The velocity field of stationary, turbulent, twin round jets has been found to scale with an intrinsic velocity 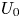$U_0$ and length 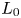$L_0$, both depending linearly on inflow plane parameters – jet velocity 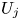$U_j$, diameter 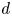$d$ and distance between jets 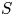$S$. Flow fields were obtained from large-eddy simulations at these conditions in two experiments: (1) at Reynolds number 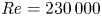${Re}=230\,000$ based on 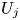$U_j$ and 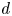$d$, and 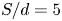$S/d=5$; and (2) at 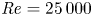${Re} = 25\,000$, 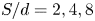$S/d = 2, 4, 8$. Each jet develops independently and then merges into a single jet with an elliptic cross-section. Downstream, the jet becomes circular after a mild overshoot. Close quantitative agreement with experiment was obtained in all cases. As the merged jets develop, fluctuation levels over a central half-width are nearly uniform and scale with the local maximum mean velocity. In all cases, the mean streamwise velocity along the centreline of the configuration, 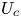$U_c$, rises to a peak 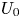$U_0$ at a distance 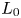$L_0$ from the inflow plane. The velocity 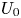$U_0$ decreases and 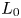$L_0$ increases with 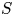$S$. For all nozzle spacings, a similar development was observed: 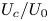$U_c/U_0$ is a function of distance 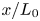$x/L_0$ only, and is essentially independent of 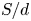$S/d$ and 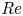${Re}$. Further, these intrinsic and input quantities are connected by simple relations: 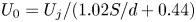$U_0 = U_j/(1.02S/d + 0.44)$ and 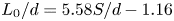$L_0/d = 5.58S/d - 1.16$. The far field development of the merged jet can also be scaled with 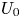$U_0$ and 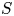$S$, analogous to round jet scaling with 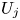$U_j$ and 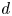$d$. Thus all twin round jets may be described by these new intrinsic scales.

We report on the presence of the boundary zonal flow in rotating Rayleigh–Bénard convection evidenced by two-dimensional particle image velocimetry. Experiments were conducted in a cylindrical cell of aspect ratio $\varGamma =D/H=1$ between its diameter ($D$) and height ($H$). As the working fluid, we used various mixtures of water and glycerol, leading to Prandtl numbers in the range $6.6 \lesssim \textit {Pr} \lesssim 76$. The horizontal velocity components were measured at a horizontal cross-section at half height. The Rayleigh numbers were in the range $10^8 \leq \textit {Ra} \leq 3\times 10^9$. The effect of rotation is quantified by the Ekman number, which was in the range $1.5\times 10^{-5}\leq \textit {Ek} \leq 1.2\times 10^{-3}$ in our experiment. With our results we show the first direct measurements of the boundary zonal flow (BZF) that develops near the sidewall and was discovered recently in numerical simulations as well as in sparse and localized temperature measurements. We analyse the thickness $\delta _0$ of the BZF as well as its maximal velocity as a function of Pr, Ra and Ek, and compare these results with previous results from direct numerical simulations.

We investigate the effects of the turbulent dynamic range on active scalar mixing in stably stratified turbulence by adapting the theoretical passive scalar modelling arguments of Beguier, Dekeyser & Launder (1978) (Phys. Fluids, vol. 21 (3), pp. 307–310) and demonstrating their usefulness through consideration of the results of direct numerical simulations of statistically stationary homogeneous stratified and sheared turbulence. By analysis of inertial and inertial–convective subrange scalings, we show that the relationship between the active scalar and turbulence time scales is predicted by the ratio of the Kolmogorov and Obukhov–Corrsin constants, provided mean flow parameters permit the two subrange scalings to be appropriate approximations. We use the resulting relationship between time scales to parameterise an appropriate turbulent mixing coefficient $\varGamma \equiv \chi /\epsilon$, defined here as the ratio of available potential energy ($E_p$) and turbulent kinetic energy ($E_k$) dissipation rates. With the analysis presented here, we show that $\varGamma$ can be estimated by $E_p,E_k$ and a universal constant provided an appropriate Reynolds number is sufficiently high. This large Reynolds number regime appears here to occur at $ {{Re_b}} \equiv \epsilon / \nu N^{2} \gtrapprox 300$ where $\nu$ is the kinematic viscosity and $N$ is the characteristic buoyancy frequency. We propose a model framework for irreversible diapycnal mixing with robust theoretical parametrisation and asymptotic behaviour in this high-$ {{Re_b}}$ limit.

Moderate rotation and moderate horizontal confinement similarly enhance the heat transport in Rayleigh–Bénard convection (RBC). Here, we systematically investigate how these two types of flow stabilization together affect the heat transport. We conduct direct numerical simulations of confined-rotating RBC in a cylindrical set-up at Prandtl number $\textit {Pr}=4.38$, and various Rayleigh numbers $2\times 10^{8}\leqslant {\textit {Ra}}\leqslant 7\times 10^{9}$. Within the parameter space of rotation (given as inverse Rossby number $0\leqslant {\textit {Ro}}^{-1}\leqslant 40$) and confinement (given as height-to-diameter aspect ratio $2\leqslant \varGamma ^{-1}\leqslant 32$), we observe three heat transport maxima. At lower $ {\textit {Ra}}$, the combination of rotation and confinement can achieve larger heat transport than either rotation or confinement individually, whereas at higher $ {\textit {Ra}}$, confinement alone is most effective in enhancing the heat transport. Further, we identify two effects enhancing the heat transport: (i) the ratio of kinetic and thermal boundary layer thicknesses controlling the efficiency of Ekman pumping, and (ii) the formation of a stable domain-spanning flow for an efficient vertical transport of the heat through the bulk. Their interfering efficiencies generate the multiple heat transport maxima.

We show that in the linear approximation there are three classes of reflectionless wave propagation on a surface of shallow water in the channel with spatially varying depth, width and current speed. Two of these classes have been described in our previous paper (Churilov & Stepanyants, J. Fluid Mech., vol. 931, 2022, A15), and the third one was discovered recently and is described here. The general analysis of the problem shows that, within the approach used in both of our papers, these three classes apparently exhaust all possible cases of exact solutions of the problem considered. We show that the reflectionless flow can be global for certain conditions, i.e. it can exist on the entire $x$-axis. There are also reflectionless flows which exist only on limited intervals of the $x$-axis.

This article presents a data-driven model based on modal decomposition, applied to approximate the low-order statistics of the spatially averaged wall-shear stress in a turbulent channel flow over a porous wall with two anisotropic permeabilities, producing drag increase or reduction when compared with the case of an isotropic porous wall. The model is comparable to a neural network architecture using a linear map to a classification. To create this model, we use high-order dynamic mode decomposition (DMD) to identify the structures describing the main flow dynamics, and then test different linear combinations of these modes to estimate the time evolution of the stress at the porous interface. The coefficients of the model are obtained by training the model against the results of direct numerical simulations over different time intervals. Depending on the number and the way of combining the DMD modes, the reduced-order models presented can reconstruct the wall-shear stress with relative error smaller than 0.01 % and reproduce its statistical variations for at least 1500 time units with relative error in the standard deviation or the mean smaller than 5 %. The model has also been tested to approximate the statistics of the wall-shear stress over the whole wall, showing that the regeneration of the flow structures can be reproduced by the nonlinear interaction of modes. Finally, considering the DMD modes as communities in a neural network, we examine the influence of the mode-to-mode interaction on the nonlinear flow dynamics, which explains the performance of the different models.

The interplay between convective, rotational and magnetic forces defines the dynamics within the electrically conducting regions of planets and stars. Yet their triadic effects are separated from one another in most studies, arguably due to the richness of each subset. In a single laboratory experiment, we apply a fixed heat flux, two different magnetic field strengths and one rotation rate, allowing us to chart a continuous path through Rayleigh–Bénard convection (RBC), two regimes of magnetoconvection, rotating convection and two regimes of rotating magnetoconvection, before finishing back at RBC. Dynamically rapid transitions are determined to exist between jump rope vortex states, thermoelectrically driven magnetoprecessional modes, mixed wall- and oscillatory-mode rotating convection and a novel magnetostrophic wall mode. Thus, our laboratory ‘pub crawl’ provides a coherent intercomparison of the broadly varying responses arising as a function of the magnetorotational forces imposed on a liquid-metal convection system.

The impact of flexible rectangular aluminum plates on a quiescent water surface is studied experimentally. The plates are mounted via pinned supports at the leading and trailing edges to an instrument carriage that drives the plates at constant velocity and various angles relative to horizontal into the water surface. Time-resolved measurements of the hydrodynamic normal force ($F_n$) and transverse moment ($M_{to}$), the spray root position ($\xi _r$) and the plate deflection ($\delta$) are collected during plate impacts at 25 experimental conditions for each plate. These conditions comprise a matrix of impact Froude numbers ${Fr} = V_n(gL)^{-0.5}$, plate stiffness ratios $R_D= \rho _w V_n^2 L^3D^{-1}$ and submergence time ratios $R_T= T_sT_{1w}^{-1}$. It is found that $R_D$ is the primary dimensionless ratio controlling the role of flexibility during the impact. At conditions with low $R_D$, maximum plate deflections on the order of $1$ mm occur and the records of the dimensionless form of $F_n$, $M_{to}$, $\xi _r$ and $\delta _c$ are nearly identical when plotted vs $tT_s^{-1}$. In these cases, the impact occurs over time scales substantially greater than the plate's natural period, and a quasi-static response ensues with the maximum deflection occurring approximately midway through the impact. For conditions with higher $R_D$ ($\gtrsim 1.0$), the above-mentioned dimensionless quantities depend strongly on $R_D$. These response features indicate a dynamic plate response and a two-way fluid–structure interaction in which the deformation of the plate causes significant changes in the hydrodynamic force and moment.

We numerically investigate turbulent Rayleigh–Bénard convection through two immiscible fluid layers, aiming to understand how the layer thickness and fluid properties affect the heat transfer (characterized by the Nusselt number $\mbox {Nu}$) in two-layer systems. Both two- and three-dimensional simulations are performed at fixed global Rayleigh number $\mbox {Ra}=10^8$, Prandtl number $\mbox {Pr}=4.38$ and Weber number $\mbox {We}=5$. We vary the relative thickness of the upper layer between $0.01 \le \alpha \le 0.99$ and the thermal conductivity coefficient ratio of the two liquids between $0.1 \le \lambda _k \le 10$. Two flow regimes are observed. In the first regime at $0.04\le \alpha \le 0.96$, convective flows appear in both layers and $\mbox {Nu}$ is not sensitive to $\alpha$. In the second regime at $\alpha \le 0.02$ or $\alpha \ge 0.98$, convective flow only exists in the thicker layer, while the thinner one is dominated by pure conduction. In this regime, $\mbox {Nu}$ is sensitive to $\alpha$. To predict $\mbox {Nu}$ in the system in which the two layers are separated by a unique interface, we apply the Grossmann–Lohse theory for both individual layers and impose heat flux conservation at the interface. Without introducing any free parameter, the predictions for $\mbox {Nu}$ and for the temperature at the interface agree well with our numerical results and previous experimental data.

The motion of finite-length cylindrical rods moving near a planar rigid surface is a scenario common across many engineering and natural settings. We study the low-Reynolds-number flow around finite rods that are allowed to rotate or translate in directions perpendicular or parallel to the plane. We develop a three-dimensional lubrication theory to characterize the pressure and hydrodynamic resistances of the cylinders through a special consideration of the cylinder's end effects. In addition, we use three-dimensional numerical simulations to solve these Stokes flows for cylinders of varying lengths and with varying gap sizes between the cylinder and plane, and the numerical results support the developed analytical descriptions. We also use visualizations of the flow to provide qualitative insights and rationalize the effect of the ends on the dynamics of the cylinders. The numerical simulations and theoretical predictions show good agreement in the long (isolated ends) and short (disk-like) limits.

An unsteady analytical solution is proposed to predict the spreading rate of the crown generated by an impacting droplet onto wetted walls. The modelling strategy is based on the direct integration of the boundary layer correction into the potential flow solution that leads to the well-established square-root time dependence. The original potential flow has the structure of an unsteady, stagnation point flow with decaying strength. For initial strengths of the potential flow $a_0 \geqslant 100\ {\rm s}^{-1}$, we find that a self-similar solution can also be obtained for the boundary layer in the variables $\left (r \sqrt {a(t)/(\nu t)}, z \sqrt {a(t)/(\nu t)} \right )$. The self-similarity of the solution enables a straightforward estimation of momentum losses during the spreading of the liquid layer along the wall. The proposed modelling approach yields an excellent agreement with experiments during the entire spreading phase. Moreover, it enables a smooth transition from the inertia-driven to the shear-controlled regime of crown propagation. In general, the analysis shows that momentum losses arising from viscous effects cannot be neglected during a significant portion of crown propagation, particularly for thin wall films.

In this paper, slip at liquid–liquid interfaces is studied focusing on the ubiquitous case in which a third species (e.g. a gas) is present. Non-equilibrium molecular dynamics simulations demonstrate that the contaminant species accumulate at the liquid–liquid interface, enriching it and affecting momentum transfer in a non-trivial fashion. The Navier boundary condition is seen to apply at this interface, accounting for slip between the liquids. Opposite trends are observed for soluble and poorly soluble species, with the slip length decreasing with concentration in the first case and significantly increasing in the latter. Two regimes are found, one in which the liquid–liquid interface is altered by the third species but changes in slip length remain limited to molecular sizes (intrinsic slip). In the second regime, further accumulation of non-soluble gas at the interface gives rise to a gaseous layer replacing the liquid–liquid interface; in this case, the apparent slip lengths are one order of magnitude larger and grow linearly with the layer width as captured quantitatively by a simple three-fluids model. Overall, results show that the presence of a third species considerably enriches the slip phenomenology both calling for new experiments and opening the door to novel strategies to control liquid–liquid slip, e.g. in liquid infused surfaces.

In this paper, we study the role of shear-induced migration and particle-induced normal stresses in the formation and stability of a particle-laden, gravity-driven shallow flow. We first examine the modification of the base-state Nusselt flow due to the underlying microstructure, how shear-induced migration leads to viscosity stratification. We inspect the development of the base state via the boundary layer formation in the ‘shallow’ limit and find a reduction in entrance length with increasing bulk particle concentration and an increase in entrance length with increasing Péclet number ($Pe_p = \dot {\gamma } a^2 / D_0$, where $\dot{\gamma}$ is the average shear rate, a is the particle size and $D_0$ is the single particle diffusivity). A linear stability analysis is then performed on the fully developed state to identify two modes of instability typically found in gravity-driven falling films – the long-wave surface and the short-wave shear modes. We find that when the associated Péclet number is $Pe_p \ll 1$, increasing bulk particle volume fraction delays the onset of instability for both the surface mode and shear mode. However, with $Pe_p = {O}(1)$, we find an enhancement in both modes of instability. We also find that, beyond a critical Péclet number, for a fixed particle volume fraction, the surface mode is unstable even in the absence of fluid inertia. The enhanced destabilisation is attributed to the combined effects of base-state viscosity stratification and momentum forcing via particle concentration perturbations. We also show that the physics behind the enhancement of instability is independent of the choice of the constitutive model used to describe the dynamics of the particle phase, provided the chosen model has elements of shear-induced migration.

A physical description of the flow mechanisms that govern the distribution of the wall-pressure fluctuations over the surface of a serrated trailing edge is proposed. Three main mechanisms that define the variation of turbulent pressure fluctuations across the serrated edge are discussed and semi-empirical models are formulated accordingly. It is shown that the intensity of the wall-pressure fluctuations increases at the tips under the effect of an increased convective velocity as a result of sidewise momentum diffusion. Furthermore, the change of impedance across the edge causes a local reduction of the pressure fluctuations in the vicinity of the trailing edge. Finally, aerodynamic loading over the serrations due to the non-symmetric flow created at different angles of attack establishes secondary flow patterns that induce higher wall-pressure fluctuations over the serration edges. The latter effect is present only for serrations under high aerodynamic loading, while the former ones are observed under any conditions. Semi-empirical models are formulated for predicting the variation of the wall-pressure fluctuations over the serration surface based on the three physical mechanisms described. These models are calibrated and compared against experiments conducted on a symmetric airfoil model at high Reynolds numbers.

Meandering channels are dynamic landforms that arise as a result of fluid mechanic and sedimentary processes. Their evolution has been described by the meander-morphodynamic equations, which dictate that channel curvature and bed topography give rise to local perturbations in streamwise fluid velocity, prompting the preferential erosion and sediment deposition that constitute meander behaviour. Novel mathematical conditions are presented to guarantee unique solutions for the linearized equations in non-periodic domains with finite boundaries. With the boundary condition specification sufficient for the uniqueness proof one finds a well-posed initial-boundary-value problem amenable to standard numerical techniques for partial differential equations. This provides a pathway for improved numerical algorithms for simulations of meandering river dynamics. Previous theoretical analysis for linear stability theory in meandering dynamics has been restricted to spatially periodic systems. The present effort develops new results for linear stability theory in non-periodic systems with temporal driving at system boundaries as well as non-homogeneous initial conditions. Predictions for temporal driving at the inlets for non-periodic finite domains provide clarification for observed behaviour in laboratory flumes where driven conditions at the inlet avoids the long-term decay of all meanders observed in flumes with fixed entry conditions. Linear stability theory for finite domains confirms that a continuous perturbation is required for sustained meandering. Original scaling arguments are presented for the dependence of the meander migration rate on geological parameters, showing that the rate of channel migration increases with increased width, downreach slope and bank erodibility, and decreases with increased volumetric flow rate.

Capillary flow of liquids plays a key role in many applications including lab-on-a-chip devices, heat pipes and printed electronics manufacturing. Open rectangular microchannels often appear in these applications, with the lack of a top resulting in a complex free-surface morphology and evaporation. In this work we develop a theoretical model based on lubrication theory and kinetically limited evaporation to examine capillary flow of evaporating liquid solutions in open rectangular microchannels connected to circular reservoirs. The model accounts for the complex free-surface morphology, solvent evaporation, Marangoni flows due to gradients in solute concentration and temperature and finite-size reservoir effects. Significant differences are predicted in flow behaviour between pure liquids and liquid solutions due to solvent evaporation and solute transport. Marangoni flows are found to promote more uniform solute deposition patterns after solvent evaporation. Model predictions of meniscus position evolution are in good agreement with prior capillary-flow experiments of aqueous poly(vinyl alcohol) solutions in the presence of evaporation. The model reveals that the principal mechanism through which evaporation influences the meniscus position in the experiments is the increase in viscosity with solute concentration.

The onset and evolution of the dynamic stall vortex (DSV) are analysed by means of large eddy simulations of an SD7003 aerofoil undergoing periodic plunging motion in a transitional Reynolds number flow ($Re =6\times 10^{4}$). Interactions between upstream propagating Kelvin–Helmholtz instabilities and a shear layer formed at the leading edge trigger flow separation. The former appear to be related to acoustic waves scattered at the trailing edge due to initial vortex shedding. Two freestream Mach numbers ($M_{\infty }=0.1$ and $0.4$) are employed to examine the flow differences due to compressibility variations. The existence of a common timing for the acoustic perturbations in both flows suggests a possible Mach number invariance for the birth of the Kelvin–Helmholtz instability. Increasing compressibility, however, induces earlier spanwise fluctuations, higher flow three-dimensionality and a weaker and more diffuse DSV, which is formed further downstream of the leading edge and has lower residency time. In order to better characterize the onset of the DSV, two empirical criteria are assessed: the leading edge suction parameter and the chord-normal shear layer height. Results demonstrate a higher robustness of the latter with respect to Mach number variations. Modal decomposition, performed with both the classical dynamic mode decomposition (DMD) and its multi-resolution variant (mrDMD), highlights key trends and demonstrates the capacity of the mrDMD to extract physically meaningful flow structures related to the stall onset. Such detailed characterization of the shear layer can be used for a systematic exploration of flow control strategies for unsteady aerofoils.

The effect of electrostatic forces on the dispersion of small like-charged inertial particles transported by a homogeneous isotropic turbulent flow is analysed by means of direct numerical simulations coupled with the Lagrangian tracking of charged particles. The results show that particle dispersion decreases for increasing charge. Since turbulent particle dispersion is related to the intensity of particle agitation and to the Lagrangian particle integral time scale, we analyse the effects of electrostatic forces on these two quantities. Particle agitation decreases for increasing particle charge. In fact, particle kinetic energy is not directly modified by electrostatic forces, which are conservative, it is rather the particle entrainment by fluid turbulence that is modified. To support this claim, one shows that the fluid–particle velocity covariance is destructed by electrostatic forces, a destruction can be predicted by drawing an analogy between inter-particle collisions and Coulomb collisions. As expected, electrostatic forces decorrelate particle velocities leading to a decrease of the Lagrangian particle integral time scale. Finally, one shows that the analogy with inter-particle collisions allows us to predict the reduction of particle dispersion.

We develop coupled evolution equations for viscous fingering (VF) and phase separation in partially miscible systems by combining a simple double-well thermodynamic free energy and Korteweg force with a classical miscible VF model for a binary system. The VF pattern transition into a droplet formation pattern by the spinodal decomposition effect is demonstrated, and the simultaneous increases in the depth of the energy minimum, in the difference in the equilibrium concentrations, and in the Korteweg force, enhance the droplet growth. The pattern's interfacial length increases with the spinodal decomposition effects. These results match the corresponding experimental results.

We report experimental and theoretical results on how a fluid (homogeneous or continuously stratified) is spun up in a closed, semicircular cylinder. Experiments were performed for Rossby numbers $Ro=0.02$, 0.2 and 1 (the latter corresponding to the limiting case of spin-up from rest), with the Ekman number $E=O({10^{-5}})$, and the Burger number ($S$) varied between 0 and 10. There are two key processes: Ekman pumping that drives the core flow; and the formation and breakdown of the vertical-wall boundary layers, with respective characteristic time scales $t\sim E^{-1/2}$ and $Ro^{-1}$. When these time scales are comparable, the observed flow is dominated by the gradual spin-up of the initial anticyclone that forms when the rotation rate is increased, which fills the container's interior; vorticity generated adjacent to the vertical walls throughout remains confined to the neighbourhood of the container's walls and corners. Conversely, when ${E^{1/2}/Ro\ll 1}$, the vertical-wall boundary layers rapidly break down, resulting in the formation of cyclonic vortices in the container's vertical corners, which grow and interact with the initial anticyclone, leading to the formation of a three-cell flow pattern. For $Ro=0.02$, our theoretical description of the flow generally agrees well with experiments, and the computation of the eruption times for the unsteady boundary layers is consistent with the observations for both $Ro=0.02$ and $Ro=0.2$.