We consider the solidification of idealised two-component mixtures comprising a solvent or suspending fluid and dissolved solute molecules or suspended colloidal particles, each considered as hard spheres. We review some fundamental thermodynamic ideas regarding relative motion between species and phase equilibria in such mixtures to show how the related solid–liquid phase diagrams depend on the size of the spheres. Using similarity solutions, we first describe freezing of the solvent to form a pure solid (here referred to as ‘ice’), with the solute rejected from the solid forming a boundary layer or dense particle layer ahead of the freezing front. We extend ideas of constitutional supercooling to the case of colloidal suspensions and show that, for a given temperature difference driving solidification, constitutional supercooling occurs only for an intermediate range of particle sizes. Constitutional supercooling promotes the formation of a mushy layer in which segregated ice separates regions of concentrated solute or particles on the microscale. We formulate a continuum model of the mushy layer that relies on a key observation that the regelative motion of concentrated clusters of particles is independent of the size and geometry of the cluster. Our modelling begins with a description of relative motion as a Fickian diffusive process. However, at high particle concentrations, we show that it is more convenient and more computationally tractable to use an equivalent formulation in terms of Darcy flow of the solvent. Within a mushy layer these diffusive fluxes correspond directly to the regelative flux of particle clusters at a rate determined by the local temperature and temperature gradient.

Circular milling, a stunning manifestation of collective motion, is found across the natural world, from fish shoals to army ants. It has been observed recently that the plant-animal worm Symsagittifera roscoffensis exhibits circular milling behaviour, both in shallow pools at the beach and in Petri dishes in the laboratory. Here we investigate this phenomenon experimentally and theoretically, from a fluid dynamical viewpoint, focusing on the effect that an established circular mill has on the surrounding fluid. Unlike systems such as confined bacterial suspensions and collections of molecular motors and filaments that exhibit spontaneous circulatory behaviour, and which are modelled as force dipoles, the front–back symmetry of individual worms precludes a stresslet contribution. Instead, singularities such as source dipoles and Stokes quadrupoles are expected to dominate. We analyse a series of models to understand the contributions of these singularities to the azimuthal flow fields generated by a mill, in light of the particular boundary conditions that hold for flow in a Petri dish. A model that treats a circular mill as a rigid rotating disc that generates a Stokes flow is shown to capture basic experimental results well, and gives insights into the emergence and stability of multiple mill systems.

We revisit the dynamics of a thick liquid film flowing down a vertical fibre. Instead of deriving a long-wave model, we directly solve the Navier–Stokes equations using a domain mapping technique and the exact steady travelling wave solutions are explored using a dynamical systems theory approach. Three distinct flow regimes, labelled ‘a’, ‘b’ and ‘c’, observed in previous experiments (Kliakhandler et al., J. Fluid Mech., vol. 429, 2001, pp. 381–390) are investigated. Flow regime ‘a’ refers to a steady flow state in which large droplets are separated by a long thin film. Flow regime ‘b’ is a necklace-like flow. In flow regime ‘c’, a cyclic process of droplet coalescence and breakup was observed. By matching the mean flow rates of the travelling wave solutions and experimental data, our travelling wave solutions show an excellent agreement with flow regimes ‘a’ and ‘b’. The time-periodic flow regime ‘c’ is compared with direct numerical simulation of the Navier–Stokes equations. A snapshot of the simulation shows a remarkable similarity to an experimental image and the discrepancy of mean wave speed and maximal wave height between our numerical simulation and experimental data is negligible.

In this work, model closures of the multiphase Reynolds-averaged Navier–Stokes (RANS) equations are developed for homogeneous, fully developed gas–particle flows. To date, the majority of RANS closures are based on extensions of single-phase turbulence models, which fail to capture complex two-phase flow dynamics across dilute and dense regimes, especially when two-way coupling between the phases is important. In the present study, particles settle under gravity in an unbounded viscous fluid. At sufficient mass loadings, interphase momentum exchange between the phases results in the spontaneous generation of particle clusters that sustain velocity fluctuations in the fluid. Data generated from Eulerian–Lagrangian simulations are used in a sparse regression method for model closure that ensures form invariance. Particular attention is paid to modelling the unclosed terms unique to the multiphase RANS equations (drag production, drag exchange, pressure strain and viscous dissipation). A minimal set of tensors is presented that serve as the basis for modelling. It is found that sparse regression identifies compact, algebraic models that are accurate across flow conditions and robust to sparse training data.

Motivated by the desire to understand complex transient behaviour in fluid flows, we study the dynamics of an air bubble driven by the steady motion of a suspending viscous fluid within a Hele-Shaw channel with a centred depth perturbation. Using both experiments and numerical simulations of a depth-averaged model, we investigate the evolution of an initially centred bubble of prescribed volume as a function of flow rate and initial shape. The experiments exhibit a rich variety of organised transient dynamics, involving bubble breakup as well as aggregation and coalescence of interacting neighbouring bubbles. The long-term outcome is either a single bubble or multiple separating bubbles, positioned along the channel in order of increasing velocity. Up to moderate flow rates, the life and fate of the bubble are reproducible and can be categorised by a small number of characteristic behaviours that occur in simply connected regions of the parameter plane. Increasing the flow rate leads to less reproducible time evolutions with increasing sensitivity to initial conditions and perturbations in the channel. Time-dependent numerical simulations that allow for breakup and coalescence are found to reproduce most of the dynamical behaviour observed experimentally, including enhanced sensitivity at high flow rate. An unusual feature of this system is that the set of steady and periodic solutions can change during temporal evolution because both the number of bubbles and their size distribution evolve due to breakup and coalescence events. Calculation of stable and unstable solutions in the single- and two-bubble cases reveals that the transient dynamics is orchestrated by weakly unstable solutions of the system that can appear and disappear as the number of bubbles changes.

Direct numerical simulations have been performed for turbulent thermal convection between horizontal no-slip, permeable walls with a distance 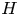$H$ and a constant temperature difference 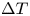$\Delta T$ at the Rayleigh number 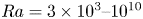$Ra=3\times 10^3\text {--}10^{10}$. On the no-slip wall surfaces $z=0$, $H$, the wall-normal (vertical) transpiration velocity is assumed to be proportional to the local pressure fluctuation, i.e. 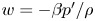$w=-\beta p'/\rho$, 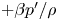$+\beta p'/\rho$ (Jiménez et al., J. Fluid Mech., vol. 442, 2001, pp. 89–117). Here 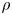$\rho$ is mass density, and the property of the permeable wall is given by the permeability parameter 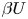$\beta U$ normalised with the buoyancy-induced terminal velocity 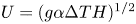$U=(g\alpha \Delta TH)^{1/2}$, where 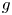$g$ and 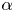$\alpha$ are acceleration due to gravity and volumetric thermal expansivity, respectively. The critical transition of heat transfer in convective turbulence has been found between the two 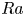$Ra$ regimes for fixed 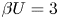$\beta U=3$ and fixed Prandtl number 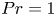$Pr=1$. In the subcritical regime at lower 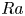$Ra$ the Nusselt number 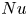$Nu$ scales with 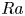$Ra$ as 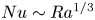$Nu\sim Ra^{1/3}$, as commonly observed in turbulent Rayleigh–Bénard convection. In the supercritical regime at higher 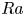$Ra$, on the other hand, the ultimate scaling 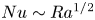$Nu\sim Ra^{1/2}$ is achieved, meaning that the wall-to-wall heat flux scales with 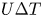$U\Delta T$ independent of the thermal diffusivity, although the heat transfer on the wall is dominated by thermal conduction. In the supercritical permeable case, large-scale motion is induced by buoyancy even in the vicinity of the wall, leading to significant transpiration velocity of the order of 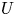$U$. The ultimate heat transfer is attributed to this large-scale significant fluid motion rather than to transition to turbulence in boundary-layer flow. In such ‘wall-bounded’ convective turbulence, a thermal conduction layer still exists on the wall, but there is no near-wall layer of large change in the vertical velocity, suggesting that the effect of the viscosity is negligible even in the near-wall region. The balance between the dominant advection and buoyancy terms in the vertical Boussinesq equation gives us the velocity scale of 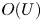$O(U)$ in the whole region, so that the total energy budget equation implies the Taylor dissipation law 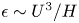$\epsilon \sim U^3/H$ and the ultimate scaling 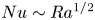$Nu\sim Ra^{1/2}$.

For a small sessile or pendant droplet it is generally assumed that gravity does not play any role once the Bond number is small. This is even assumed for evaporating binary sessile or pendant droplets, in which convective flows can be driven due to selective evaporation of one component and the resulting concentration and thus surface tension differences at the air–liquid interface. However, recent studies have shown that in such droplets gravity indeed can play a role and that natural convection can be the dominant driving mechanism for the flow inside evaporating binary droplets (Edwards et al., Phys. Rev. Lett., vol. 121, 2018, 184501; Li et al., Phys. Rev. Lett., vol. 122, 2019, 114501). In this study, we derive and validate a quasi-stationary model for the flow inside evaporating binary sessile and pendant droplets, which successfully allows one to predict the prevalence and the intriguing interaction of Rayleigh and/or Marangoni convection on the basis of a phase diagram for the flow field expressed in terms of the Rayleigh and Marangoni numbers.

Electrohydrodynamics of drops is a classic fluid mechanical problem where deformations and microscale flows are generated by application of an external electric field. In weak fields, electric stresses acting on the drop surface drive quadrupolar flows inside and outside and cause the drop to adopt a steady axisymmetric shape. This phenomenon is best explained by the leaky-dielectric model under the premise that a net surface charge is present at the interface while the bulk fluids are electroneutral. In the case of dielectric drops, increasing the electric field beyond a critical value can cause the drop to start rotating spontaneously and assume a steady tilted shape. This symmetry-breaking phenomenon, called Quincke rotation, arises due to the action of the interfacial electric torque countering the viscous torque on the drop, giving rise to steady rotation in sufficiently strong fields. Here, we present a small-deformation theory for the electrohydrodynamics of dielectric drops for the complete Melcher–Taylor leaky-dielectric model in three dimensions. Our theory is valid in the limits of strong capillary forces and highly viscous drops and is able to capture the transition to Quincke rotation. A coupled set of nonlinear ordinary differential equations for the induced dipole moments and shape functions are derived whose solution matches well with experimental results in the appropriate small-deformation regime. Retention of both the straining and rotational components of the flow in the governing equation for charge transport enables us to perform a linear stability analysis and derive a criterion for the applied electric field strength that must be overcome for the onset of Quincke rotation of a viscous drop.

Rotating Rayleigh–Bénard convection is investigated numerically with the use of an asymptotic model that captures the rapidly rotating, small Ekman number limit, $Ek \rightarrow 0$. The Prandtl number ($Pr$) and the asymptotically scaled Rayleigh number ($\widetilde {Ra} = Ra Ek^{4/3}$, where $Ra$ is the typical Rayleigh number) are varied systematically. For sufficiently vigorous convection, an inverse kinetic energy cascade leads to the formation of a pair of large-scale vortices of opposite polarity, in agreement with previous studies of rapidly rotating convection. With respect to the kinetic energy, we find a transition from convection dominated states to a state dominated by large-scale vortices at an asymptotically reduced (small-scale) Reynolds number of $\widetilde {Re} \approx 6$ ($\widetilde {Re} = Re Ek^{1/3}$, where $Re$ is the Reynolds number associated with vertical flows) for all investigated values of $Pr$. The ratio of the depth-averaged kinetic energy to the kinetic energy of the convection reaches a maximum at $\widetilde {Re} \approx 24$, then decreases as $\widetilde {Ra}$ is increased. This decrease in the relative kinetic energy of the large-scale vortices is associated with a decrease in the convective correlations with increasing Rayleigh number. The scaling behaviour of the convective flow speeds is studied; although a linear scaling of the form $\widetilde {Re} \sim \widetilde {Ra}/Pr$ is observed over a limited range in Rayleigh number and Prandtl number, a clear departure from this scaling is observed at the highest accessible values of $\widetilde {Ra}$. Calculation of the forces present in the governing equations shows that the ratio of the viscous force to the buoyancy force is an increasing function of $\widetilde {Ra}$, that approaches unity over the investigated range of parameters.

The phenomena of self-sustained shock-wave oscillations over conical bodies with a blunt axisymmetric base subject to uniform high-speed flow are investigated in a hypersonic wind tunnel at Mach number $M = 6$. The flow and shock-wave dynamics is dictated by two non-dimensional geometric parameters presented by the three length scales of the body, two of which are associated with the conical forebody and one with the base. Time-resolved schlieren imagery from these experiments reveals the presence of two disparate states of shock-wave oscillations in the flow, and allows for the mapping of unsteadiness boundaries in the two-parameter space. Physical mechanisms are proposed to explain the oscillations and the transitions of the shock-wave system from steady to oscillatory states. In comparison with the canonical single-parameter problem of shock-wave oscillations over spiked-blunt bodies reported in literature, the two-parameter nature of the present problem introduces distinct elements to the flow dynamics.

The dynamics of intense vorticity is investigated by means of synchronisation experiments in direct numerical simulations of isotropic turbulence. By imposing similar dynamics above the dissipative range, the same structures of intense vorticity appear in two independent turbulent flows, showing that intense vorticity synchronises to large-scale dynamics. Remarkably, this synchronisation takes place despite the presence of chaos, and affects mostly the intense vorticity, but not so much the weak vorticity background, which remains comparatively asynchronous. These results pinpoint the role of large-scale dynamics in the formation of intense vorticity structures, the so-called ‘worms’, and rule out the possibility that they emerge primarily due to interactions within the dissipative range, and then grow or coalesce into elongated structures. The stretching of the vorticity vector by the large-scale rate-of-strain tensor is identified as the mechanism responsible for the synchronisation of intense vorticity, supporting the extended view of vortex stretching as a fundamental inter-scale mechanism in turbulence.

This study investigates deterministic wave forecasting from the perspective of the Zakharov equation. Forecasts based on linear dispersion, weakly nonlinear amplitude dispersion and the Zakharov equation are compared for reference ocean surfaces generated from the Joint North Sea Wave Observation Project and Pierson–Moskowitz spectra. This approach allows for the role of nonlinearity to be isolated, and demonstrates the success of simple frequency corrections in forecasting wave fields up to moderate steepness. The role of second-order bound waves is investigated by means of analytical formulae, and their impact on forecast accuracy is illustrated for a range of forecast times.

Conservation laws that relate the local time-rate-of-change of the spatial integral of a density function to the divergence of its flux through the boundaries of the integration domain provide integral constraints on the spatio-temporal development of a field. Here we show that a new type of conserved quantity exists that does not require integration over a particular domain but which holds locally at any point in the field. This is derived for the pseudo-energy density of non-divergent Rossby waves where local invariance is obtained for (i) a single plane wave, and (ii) waves produced by an impulsive point source of vorticity. The definition of pseudo-energy used here consists of a conventional kinetic part, as well as an unconventional pseudo-potential part, proposed by Buchwald (Proc. R. Soc. Lond. A, vol. 328, issue 1572, 1972, pp. 37–48). The anisotropic nature of the energy flux that appears in response to the point source further clarifies the role of the beta plane in the observed western intensification of ocean currents.

Solidifying ternary systems can exhibit complex natural convection phenomena, particularly due to the presence of two porous zones (cotectic and primary mush), and the rejection of two differently dense solutes. The primary objectives of this study are to investigate the following: (i) the natural convection patterns in various compositional regimes of a typical ternary system, and (ii) the role of the combined existence of the microstructure (facets and dendrites) in the porous zone on natural convection, with a motivation to enhance the current understanding of the microstructure–convection relationships. A ternary mixture is chosen such that different compositions of the three primary solidifying components lead to the formation of distinct ice, dendritic and faceted solid structures that cover the complete span of microstructure–convection relationships. The observations of flow in different compositional regimes show convection occurring in the form of plumes, random mixing and double-diffusive layering, as well as combinations of these, which are governed by the type of coexisting microstructures. The study reveals the occurrence of Rayleigh–Taylor instability with varying amounts of the heavier component. The bulk liquid composition showed a tendency to cross the cotectic line, and thus also change the nature of primary solidifying structure from faceted to dendritic in cases where facets and dendrites were present in cotectic mush, and facets in primary mush. These insights are believed to elucidate the complex mechanisms of ternary solidification, as well as provide important real-time data for direct numerical simulations.

The three-dimensional turbulence structure of the canonical daytime atmospheric boundary layer (ABL) reflects the balance between shear and buoyancy turbulence production characterized by $-z_i/L>0$, where $z_i$ is the boundary layer height and $L<0$ is the Obukhov length. In the shear-driven neutral ABL ($-z_i/L=0$) the surface layer is characterized by coherent low-speed streaks, while the ‘moderately convective’ state ($-z_i/L\sim 1\text {--}10$) contains streamwise-elongated sheet-like updraughts. Using large-eddy simulation, we analyse the transition in ABL turbulence structure in response to systematic increases in surface heat flux and $-z_i/L$ from neutral to moderately convective. We discover a sudden change in turbulence structure at the ‘critical’ state $-z_i/L=0.433$ with nearly three-fold increase in the streamwise coherence length of ‘streaks’ at the upper surface layer and four-fold increase in the streamwise scale of updraughts in the mixed layer – as well as the initiation of spatial correlations between the two that contribute to the local generation of thermal updraughts as surface heating increases. At subcritical stability states, buoyancy impacts only the vertical thickness of the streaks. ABL receptivity to buoyancy changes when supercritical and updraughts now grow in the vertical with increasing surface heat flux; the previously amalgamated updraughts extend further in the streamwise direction. The post-critical regime is highlighted by a ‘maximum coherence state’ at $-z_i/L=1.08$ and maximally coherent ‘large-scale rolls’. At increasingly unstable states ($-z_i/L>1.08$), roll coherence decreases and the vertical scales asymptote to the canonical moderately convective ABL.

The closure of a human lung airway is modelled as a pipe coated internally with a liquid that takes into account the viscoelastic properties of mucus. For a thick-enough coating, the Plateau–Rayleigh instability blocks the airway by the creation of a liquid plug, and the preclosure phase is dominated by the Newtonian behaviour of the liquid. Our previous study with a Newtonian-liquid model demonstrated that the bifrontal plug growth consequent to airway closure induces a high level of stress and stress gradients on the airway wall, which is large enough to damage the epithelial cells, causing sublethal or lethal responses. In this study, we explore the effect of the viscoelastic properties of mucus by means of the Oldroyd-B and FENE-CR model. Viscoelasticity is shown to be very relevant in the postcoalescence process, introducing a second peak of the wall shear stresses. This second peak is related to an elastic instability due to the presence of the polymeric extra stresses. For high-enough Weissenberg and Laplace numbers, this second shear stress peak is as severe as the first one. Consequently, a second lethal or sublethal response of the epithelial cells is induced.

Wave shape (e.g. wave skewness and asymmetry) impacts sediment transport, remote sensing and ship safety. Previous work showed that wind affects wave shape in intermediate and deep water. Here, we investigate the effect of wind on wave shape in shallow water through a wind-induced surface pressure for different wind speeds and directions to provide the first theoretical description of wind-induced shape changes. A multiple-scale analysis of long waves propagating over a shallow, flat bottom and forced by a Jeffreys-type surface pressure yields a forward or backward Korteweg–de Vries (KdV)–Burgers equation for the wave profile, depending on the wind direction. The evolution of a symmetric, solitary-wave initial condition is calculated numerically. The resulting wave grows (decays) for onshore (offshore) wind and becomes asymmetric, with the rear face showing the largest shape changes. The wave profile's deviation from a reference solitary wave is primarily a bound wave and trailing, dispersive, decaying tail. The onshore wind increases the wave's energy and skewness with time while decreasing the wave's asymmetry, with the opposite holding for offshore wind. The corresponding wind speeds are shown to be physically realistic, and the shape changes are explained as slow growth followed by rapid evolution according to the unforced KdV equation.

In a theoretical analysis, we generalise well-known asymptotic results to obtain expressions for the rate of transfer of material from the surface of an arbitrary, rigid particle suspended in an open pathline flow at large Péclet number, ${Pe}$. The flow may be steady or periodic in time. We apply this result to numerically evaluate expressions for the surface flux to a freely suspended, axisymmetric ellipsoid (spheroid) in Stokes flow driven by a steady linear shear. We complement these analytical predictions with numerical simulations conducted over a range of ${Pe} = 10^1\text {--}10^4$ and confirm good agreement at large Péclet number. Our results allow us to examine the influence of particle shape upon the surface flux for a broad class of flows. When the background flow is irrotational, the surface flux is steady and is prescribed by three parameters only: the Péclet number, the particle aspect ratio and the strain topology. We observe that slender prolate spheroids tend to experience a higher surface flux compared to oblate spheroids with equivalent surface area. For rotational flows, particles may begin to spin or tumble, which may suppress or augment the convective transfer due to a realignment of the particle with respect to the strain field.

Recent simulations indicate that streamwise-preferential porous materials have the potential to reduce drag in wall-bounded turbulent flows (Gómez-de-Segura & García-Mayoral, J. Fluid Mech., vol. 875, 2019, pp. 124–172). This paper extends the resolvent formulation to study the effect of such anisotropic permeable substrates on turbulent channel flow. Under the resolvent formulation, the Fourier-transformed Navier–Stokes equations are interpreted as a linear forcing–response system. The nonlinear terms are considered the endogenous forcing in the system that gives rise to a velocity and pressure response. A gain-based decomposition of the forcing–response transfer function – the resolvent operator – identifies response modes (resolvent modes) that are known to reproduce important structural and statistical features of wall-bounded turbulent flows. The effect of permeable substrates is introduced in this framework using the volume-averaged Navier–Stokes equations and a generalized form of Darcy's law. Substrates with high streamwise permeability and low spanwise permeability are found to suppress the forcing–response gain for the resolvent mode that serves as a surrogate for the energetic near-wall cycle. This reduction in mode gain is shown to be consistent with the drag reduction trends predicted by theory and observed in numerical simulations. Simulation results indicate that drag reduction is limited by the emergence of spanwise rollers resembling Kelvin–Helmholtz vortices beyond a threshold value of wall-normal permeability. The resolvent framework also predicts the conditions in which such energetic spanwise-coherent rollers emerge. These findings suggest that a limited set of resolvent modes can serve as the building blocks for computationally efficient models that enable the design and optimization of permeable substrates for passive turbulence control.

The interaction of fluids with surface-mounted obstacles in canopy flows leads to strong turbulence that dominates dispersion and mixing in the neutrally stable atmospheric surface layer. This work focuses on intermittency in the Lagrangian velocity statistics in a canopy flow, which is observed in two distinct forms. The first, small-scale intermittency, is expressed by non-Gaussian and not self-similar statistics of the velocity increments. The analysis shows an agreement in comparison with previous results from homogeneous isotropic turbulence (HIT) using the multifractal model, extended self-similarity and velocity increments’ autocorrelations. These observations suggest that the picture of small-scale Lagrangian intermittency in canopy flows is similar to that in HIT and, therefore, they extend the idea of universal Lagrangian intermittency to certain inhomogeneous and anisotropic flows. Second, it is observed that the root mean square of energy increments along Lagrangian trajectories depends on the direction of the trajectories’ time-averaged turbulent velocity. Subsequent analysis suggests that the flow is attenuated by the canopy drag while leaving the structure function's scaling unchanged. This observation implies the existence of large-scale intermittency in Lagrangian statistics. Thus, this work presents a first empirical evidence of intermittent Lagrangian velocity statistics in a canopy flow that exists in two distinct senses and occurs due to different mechanisms.