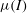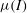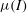Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 174
Turbulence measurements in axisymmetric jets of air and helium. Part 2. Helium jet
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 225-247
-
- Article
- Export citation
- Cited by 174
Wave capture and wave–vortex duality
-
- Published online by Cambridge University Press:
- 21 June 2005, pp. 67-95
-
- Article
- Export citation
- Cited by 174
Transverse jets and jet flames. Part 1. Scaling laws for strong transverse jets
-
- Published online by Cambridge University Press:
- 25 September 2001, pp. 1-25
-
- Article
- Export citation
- Cited by 173
Three-dimensional simulation of a flapping flag in a uniform flow
-
- Published online by Cambridge University Press:
- 02 June 2010, pp. 301-336
-
- Article
- Export citation
- Cited by 173
The complete second-order diffraction solution for an axisymmetric body Part 1. Monochromatic incident waves
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 235-264
-
- Article
- Export citation
- Cited by 173
On the acoustic levitation of droplets
-
- Published online by Cambridge University Press:
- 10 February 1998, pp. 65-91
-
- Article
- Export citation
- Cited by 173
Theoretical perspective on the route to turbulence in a pipe
-
- Published online by Cambridge University Press:
- 30 August 2016, P1
-
- Article
- Export citation
- Cited by 173
On the development of dunes in erodible channels
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 1-16
-
- Article
- Export citation
- Cited by 173
Nonlinear periodic convection in double-diffusive systems
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 291-316
-
- Article
- Export citation
- Cited by 173
The unsteady motion of a two-dimensional aerofoil in incompressible inviscid flow
-
- Published online by Cambridge University Press:
- 12 April 2006, pp. 159-178
-
- Article
- Export citation
- Cited by 173
Very-large-scale motions in a turbulent boundary layer
-
- Published online by Cambridge University Press:
- 17 February 2011, pp. 80-120
-
- Article
- Export citation
- Cited by 173
Flow past a square-section cylinder with a wavy stagnation face
-
- Published online by Cambridge University Press:
- 12 January 2001, pp. 263-295
-
- Article
- Export citation
- Cited by 173
The bifurcation of liquid bridges
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 25-39
-
- Article
- Export citation
- Cited by 173
Rheological stratification in experimental free-surface flows of granular–liquid mixtures
-
- Published online by Cambridge University Press:
- 27 May 2005, pp. 269-319
-
- Article
- Export citation
- Cited by 173
A depth-averaged
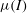 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu (I)$-rheology for shallow granular free-surface flows
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu (I)$-rheology for shallow granular free-surface flows
-
- Published online by Cambridge University Press:
- 20 August 2014, pp. 503-534
-
- Article
- Export citation
- Cited by 172
Experiments on the nonlinear stages of free-shear-layer transition
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 695-719
-
- Article
- Export citation
- Cited by 172
The instability and breaking of deep-water waves
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 165-185
-
- Article
- Export citation
- Cited by 172
Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction
-
- Published online by Cambridge University Press:
- 28 February 2012, pp. 16-28
-
- Article
- Export citation
- Cited by 172
Instability of a viscous liquid of variable density in a vertical Hele-Shaw cell
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 501-515
-
- Article
- Export citation
- Cited by 172
Flow of axisymmetric red blood cells in narrow capillaries
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 405-423
-
- Article
- Export citation