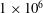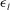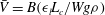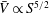Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 190
Direct numerical simulations of turbulent flows over superhydrophobic surfaces
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 31-41
-
- Article
- Export citation
- Cited by 190
Experiments on mixing due to chaotic advection in a cavity
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 463-499
-
- Article
- Export citation
- Cited by 190
Importance of the nozzle-exit boundary-layer state in subsonic turbulent jets
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 83-124
-
- Article
- Export citation
- Cited by 190
Axisymmetric deformation and stability of a viscous drop in a steady electric field
-
- Published online by Cambridge University Press:
- 15 October 2007, pp. 239-264
-
- Article
- Export citation
- Cited by 190
The behaviour of a stable salinity gradient heated from below
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 183-200
-
- Article
- Export citation
- Cited by 190
Water entry of spinning spheres
-
- Published online by Cambridge University Press:
- 14 April 2009, pp. 135-165
-
- Article
- Export citation
- Cited by 190
Flapping dynamics of an inverted flag
-
- Published online by Cambridge University Press:
- 04 November 2013, R1
-
- Article
- Export citation
- Cited by 190
The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel
-
- Published online by Cambridge University Press:
- 30 April 2008, pp. 331-365
-
- Article
- Export citation
- Cited by 190
Flow regimes of large-velocity-ratio coaxial jets
-
- Published online by Cambridge University Press:
- 25 August 1997, pp. 357-381
-
- Article
- Export citation
- Cited by 190
Long-surface-wave instability in dense granular flows
-
- Published online by Cambridge University Press:
- 24 June 2003, pp. 21-50
-
- Article
- Export citation
- Cited by 190
Aerodynamic noise from a poroelastic edge with implications for the silent flight of owls
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 456-479
-
- Article
- Export citation
- Cited by 190
Turbulent shear flow over slowly moving waves
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 109-148
-
- Article
- Export citation
- Cited by 190
On the slow motion of a sphere parallel to a nearby plane wall
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 705-724
-
- Article
- Export citation
- Cited by 190
On the transition to turbulent convection. Part 2. The transition to time-dependent flow
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 309-320
-
- Article
- Export citation
- Cited by 190
Turbulence structure in rough- and smooth-wall boundary layers
-
- Published online by Cambridge University Press:
- 14 November 2007, pp. 263-293
-
- Article
- Export citation
- Cited by 190
Air entrainment and bubble statistics in breaking waves
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 91-129
-
- Article
- Export citation
- Cited by 189
Turbulent convection in a horizontal layer of water
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 141-159
-
- Article
- Export citation
- Cited by 189
The effects of curvature in wall-bounded turbulent flows
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 479-510
-
- Article
- Export citation
- Cited by 189
The hydrodynamic stability of rapidly evaporating liquids at reduced pressure
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 487-511
-
- Article
- Export citation
- Cited by 189
MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 63-88
-
- Article
- Export citation