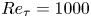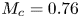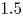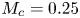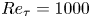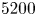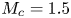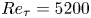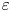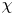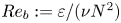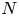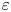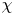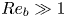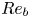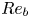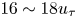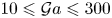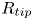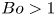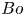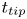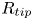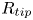Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
Turbulence in a channel with a patchy submerged canopy: the impact of spatial configuration
-
- Published online by Cambridge University Press:
- 07 March 2025, A15
-
- Article
- Export citation
- Cited by 1
A wall model for large-eddy simulation of highly compressible flows based on a new scaling of the law of the wall
-
- Published online by Cambridge University Press:
- 29 January 2024, A9
-
- Article
- Export citation
- Cited by 1
Richtmyer–Meshkov instability when a shock is reflected for fluids with arbitrary equation of state
-
- Published online by Cambridge University Press:
- 25 November 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Equilibrated crater: fragmentation and mixing
-
- Published online by Cambridge University Press:
- 13 May 2022, F1
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 1
A data-driven method for modelling dissipation rates in stratified turbulence
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2023, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Transition delay in a Mach 6 boundary layer using steady blowing and suction strips
-
- Published online by Cambridge University Press:
- 20 August 2024, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Influence of outer large-scale motions on near-wall structures in compressible turbulent channel flows
-
- Published online by Cambridge University Press:
- 18 September 2024, A14
-
- Article
- Export citation
- Cited by 1
Wave turbulence in geophysical flows
-
- Published online by Cambridge University Press:
- 27 April 2023, F1
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 1
On the dynamics and wakes of a freely settling Platonic polyhedron in a quiescent Newtonian fluid
-
- Published online by Cambridge University Press:
- 15 April 2024, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Large-scale motions in a turbulent natural convection boundary layer immersed in a stably stratified environment
-
- Published online by Cambridge University Press:
- 24 July 2023, A40
-
- Article
- Export citation
- Cited by 1
Rheological measurements and transition to turbulence for moderate Reynolds number inertial suspensions
-
- Published online by Cambridge University Press:
- 31 May 2024, A19
-
- Article
- Export citation
- Cited by 1
Gravity-coupled flutter and contact of a flag near a wall
-
- Published online by Cambridge University Press:
- 11 December 2023, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Pore-scale modelling of particle transport in a porous bed
-
- Published online by Cambridge University Press:
- 11 January 2024, A9
-
- Article
- Export citation
- Cited by 1
Fragmentation from inertial detachment of a sessile droplet: implications for pathogen transport
-
- Published online by Cambridge University Press:
- 26 December 2024, A6
-
- Article
- Export citation
- Cited by 1
Structure of mushy layers grown from perfectly and imperfectly conducting boundaries. Part 2. Onset of convection
-
- Published online by Cambridge University Press:
- 03 January 2025, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Interface coupling effect and multi-mode Faraday instabilities in a three-layer fluid system
-
- Published online by Cambridge University Press:
- 01 March 2024, A8
-
- Article
- Export citation
- Cited by 1
Perturbation analysis of baroclinic torque in low-Mach-number flows
-
- Published online by Cambridge University Press:
- 03 November 2021, A4
-
- Article
- Export citation
- Cited by 1
Low-Reynolds-number oscillating boundary layers on adiabatic slopes
-
- Published online by Cambridge University Press:
- 13 October 2022, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Effects of streamwise rotation on helicity and vortex in channel turbulence
-
- Published online by Cambridge University Press:
- 08 February 2024, A50
-
- Article
- Export citation
- Cited by 1
Experimental and numerical investigation of inertial particles in underexpanded jets
-
- Published online by Cambridge University Press:
- 27 November 2024, A60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation