Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
Shock Waves and Detonations in Gases. By R. I. SOLOUKHIN. Mono Book Corp. 1966. 176pp. $7.00.
-
- Published online by Cambridge University Press:
- 28 March 2006, p. 828
-
- Article
- Export citation
- Cited by 1
Fundamentals of Momentum, Heat and Mass Transfer. By J. R. WELTY, C. E. WICKS and R. E. WILSON. Wiley, 1976. 789 pp. $27.55. Fundamental Principles of Heat Transfer. By S. WHETAKER. Pergamon, 1977. 556 pp. $50.00.
-
- Published online by Cambridge University Press:
- 19 April 2006, pp. 793-794
-
- Article
- Export citation
- Cited by 1
Natural convection along a heated vertical plate immersed in a nonlinearly stratified medium: application to liquefied gas storage
-
- Published online by Cambridge University Press:
- 24 September 2007, pp. 217-241
-
- Article
- Export citation
- Cited by 1
Schedule of International Conferences on Fluid Mechanics
-
- Published online by Cambridge University Press:
- 10 May 1998, pp. 348-349
-
- Article
- Export citation
- Cited by 1
Thermosolutal convection in an evolving soluble porous medium
-
- Published online by Cambridge University Press:
- 26 October 2017, pp. 666-696
-
- Article
- Export citation
- Cited by 1
Quasi-cylindrical approximation to the swirling flow in an atomizer chamber
-
- Published online by Cambridge University Press:
- 10 October 2014, pp. 603-620
-
- Article
- Export citation
- Cited by 1
Multiple-scales analysis of wave evolution in the presence of rigid vegetation
-
- Published online by Cambridge University Press:
- 25 January 2022, A3
-
- Article
- Export citation
- Cited by 1
The catalytic effect of near-inertial waves on
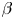 $\beta$-plane zonal jets
$\beta$-plane zonal jets
-
- Published online by Cambridge University Press:
- 04 May 2023, A33
-
- Article
- Export citation
- Cited by 1
The influence of temporal heating modulation on non-isothermal floating droplet dynamics
-
- Published online by Cambridge University Press:
- 07 October 2022, A51
-
- Article
- Export citation
- Cited by 1
Introduction to Micrometeorology (2nd edition). By S. P. ARYA. Academic Press, 2001. 420 pp. ISBN 0 12 059354 8. £ 53.95
-
- Published online by Cambridge University Press:
- 29 December 2003, pp. 441-443
-
- Article
- Export citation
- Cited by 1
Streamwise development of turbulent boundary-layer drag reduction with polymer injection
-
- Published online by Cambridge University Press:
- 25 April 2008, p. 443
-
- Article
- Export citation
- Cited by 1
Impulsively started planar actuator surfaces in high-Reynolds-number steady flow
-
- Published online by Cambridge University Press:
- 23 September 2013, pp. 302-324
-
- Article
- Export citation
- Cited by 1
Leading-edge receptivity for bodies with mean aerodynamic loading
-
- Published online by Cambridge University Press:
- 05 July 2005, pp. 1-32
-
- Article
- Export citation
- Cited by 1
Wave Flow of Liquid Films. By S. V. Alekseenko, V. E. Nakoryakov & B. G. Pokusaev. Begell, 1994. 313 pp. ISBN 1567800 0215. $135.
-
- Published online by Cambridge University Press:
- 25 May 1998, pp. 348-349
-
- Article
- Export citation
- Cited by 1
FLM volume 731 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 September 2013, pp. f1-f4
-
- Article
-
- You have access
- Export citation
- Cited by 1
Motion of open vortex-current filaments under the Biot–Savart model
-
- Published online by Cambridge University Press:
- 12 December 2017, pp. 532-559
-
- Article
- Export citation
- Cited by 1
Direct control of the small-scale energy balance in two-dimensional fluid dynamics
-
- Published online by Cambridge University Press:
- 07 October 2015, pp. 240-259
-
- Article
- Export citation
- Cited by 1
Isobath variation and trapping of continental shelf waves
-
- Published online by Cambridge University Press:
- 01 May 2012, pp. 283-303
-
- Article
- Export citation
- Cited by 1
The influence of low-conductivity boundaries on time-dependent convection
-
- Published online by Cambridge University Press:
- 24 August 2001, pp. 293-301
-
- Article
- Export citation
- Cited by 1
Discontinuous solutions of the unsteady boundary-layer equations for a rotating disk of finite radius
-
- Published online by Cambridge University Press:
- 18 March 2021, A75
-
- Article
- Export citation