Research Papers
The distribution of evolutionarily stable strategies
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 233-246
-
- Article
- Export citation
Conditions for fixation of an allele in the density-dependent wright–Fisher models
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 247-256
-
- Article
- Export citation
On solutions of a stochastic integral equation of the volterra type with applications for chemotherapy
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 257-267
-
- Article
- Export citation
A model for responding to promotion blockages
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 268-278
-
- Article
- Export citation
On passage and conditional passage times for Markov chains in continuous time
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 279-290
-
- Article
- Export citation
Pareto processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 291-301
-
- Article
- Export citation
Autoregressive processes in optimization
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 302-312
-
- Article
- Export citation
The distributional structure of finite moving-average processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 313-321
-
- Article
- Export citation
Stereological analysis of particles of varying ellipsoidal shape
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 322-335
-
- Article
- Export citation
On the distribution of points in a poisson dirichlet process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 336-345
-
- Article
- Export citation
Divided differences and the joint distribution of linear combinations of spacings
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 346-354
-
- Article
- Export citation
On the dependence structure of hitting times of univariate processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 355-362
-
- Article
- Export citation
Optimal stopping in the parking problem with U-turn
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 363-374
-
- Article
- Export citation
A non-Markov model for the optimum replacement of self-repairing systems subject to shocks
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 375-382
-
- Article
- Export citation
Some multivariate distributions derived from a non-fatal shock model
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 383-390
-
- Article
- Export citation
Regeneration in tandem queues with multiserver stations
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-403
-
- Article
- Export citation
The backlog and depletion-time process for M/G/1 vacation models with exhaustive service discipline
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 404-412
-
- Article
- Export citation
Short Communications
On higher moments of the population size in a subcritical branching process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 413-417
-
- Article
- Export citation
A time-reversibility relationship between two Markov chains with exponential stationary distributions
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 418-422
-
- Article
- Export citation
On Cox processes and gamma renewal processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 423-427
-
- Article
- Export citation

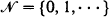 . For
. For 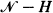 . These conditional passage times are studied through first-passage times of a modified chain
. These conditional passage times are studied through first-passage times of a modified chain 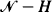 of states absorbing. It will be shown that the densities of
of states absorbing. It will be shown that the densities of 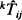 and
and 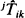 is also discussed, where
is also discussed, where 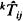 , and
, and 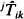 are conditional passage times of the reversed process of
are conditional passage times of the reversed process of 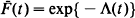 .
.