Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T07:23:20.707Z Has data issue: false hasContentIssue false
  • English
  • Français

On passage and conditional passage times for Markov chains in continuous time

Published online by Cambridge University Press:  14 July 2016

Masaaki Kijima
Masaaki Kijima*
Affiliation:
Tokyo Institute of Technology
*
∗Postal address: Department of Information Sciences, Tokyo Institute of Technology, Oh-okayama, Meguro-ku, Tokyo 152, Japan.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X(t) be a temporally homogeneous irreducible Markov chain in continuous time defined on 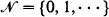. For k < i < j, let H = {k + 1, ···, j − 1} and let kTij (jTik) be the upward (downward) conditional first-passage time of X(t) from i to j(k) given no visit to 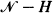. These conditional passage times are studied through first-passage times of a modified chain HX(t) constructed by making the set 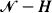of states absorbing. It will be shown that the densities of kTij and jTik for any birth-death process are unimodal and the modes kmij (jmik) of the unimodal densities are non-increasing (non-decreasing) with respect to i. Some distribution properties of kTij and jTik for a time-reversible Markov chain are presented. Symmetry among kTij, jTik, 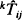and 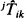is also discussed, where 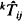, and 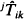are conditional passage times of the reversed process of X(t).

Keywords

FIRST PASSAGE TIMECONDITIONAL FIRST PASSAGE TIMEUNIMODALITYSYMMETRYREVERSED MARKOV CHAIN
Type
Research Papers
Information
Journal of Applied Probability , Volume 25 , Issue 2 , June 1988 , pp. 279 - 290
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Assaf, D., Shaked, M. and Shanthikumar, J. G. (1985) First-passage times with PFr densities J. Appl. Prob. 22, 185–196.CrossRefGoogle Scholar
[2] Bellman, R. E. (1960) Introduction to Matrix Analysis. McGraw-Hill, New York.Google Scholar
[3] Brown, M. and Chaganty, N. R. (1983) On the first passage time distribution for a class of Markov chains. Ann. Prob. 11, 1000–1008.Google Scholar
[4] Colquhoun, D. and Hawkes, A. G. (1982) On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Phil. Trans. R. Soc. London B300, 1–59.Google Scholar
[5] Karlin, S. (1968) Total Positivity. Stanford University Press, Stanford, CA.Google Scholar
[6] Keilson, J. (1971) Log-concavity and log-convexity in passage time densities of diffusion and birth-death processes. J. Appl. Prob. 8, 391–398.Google Scholar
[7] Keilson, J. (1979) Markov Chain Models – Rarity and Exponentiality. Springer-Verlag, New York.Google Scholar
[8] Keilson, J. (1981) On the unimodality of passage time densities in birth-death processes. Statist. Neerlandica 25, 49–55.Google Scholar
[9] Keilson, J. and Kester, A. (1978) Unimodality preservation in Markov chains. Stoch. Proc. Appl. 7, 179–190.Google Scholar
[10] Kelly, F. P. (1979) Reversibility and Stochastic Networks. Wiley, New York.Google Scholar
[11] Kemeny, J. G. and Snell, J. L. (1960) Finite Markov Chains. Von Nostrand Reinhold, New York.Google Scholar
[12] Kijima, M. (1987) Spectral structure of the first passage time densities for classes of Markov chains. J. Appl. Prob. 24, 631–643.Google Scholar
[13] Rösler, U. (1980) Unimodality of passage time densities for one-dimensional strong Markov processes. Ann. Prob. 8, 853–859.Google Scholar
[14] Seneta, E. (1981) Non-negative Matrices and Markov Chains , 2nd edn. Springer-Verlag, New York.Google Scholar
[15] Sumita, U. (1984) On conditional passage time structure of birth-death processes. J. Appl. Prob. 21, 10–21.CrossRefGoogle Scholar