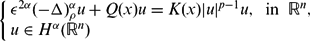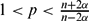Research Article
π-TYPE FERMIONS AND π-TYPE KP HIERARCHY
- Part of:
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 601-613
-
- Article
-
- You have access
- Export citation
LIFTING N-DIMENSIONAL GALOIS REPRESENTATIONS TO CHARACTERISTIC ZERO
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 115-150
-
- Article
-
- You have access
- Export citation
r-FREDHOLM THEORY IN BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 25 September 2018, pp. 615-627
-
- Article
-
- You have access
- Export citation
A STRUCTURED DESCRIPTION OF THE GENUS SPECTRUM OF ABELIAN p-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2018, pp. 381-423
-
- Article
-
- You have access
- Export citation
ON THE AXIOMATIZABILITY OF C*-ALGEBRAS AS OPERATOR SYSTEMS
-
- Published online by Cambridge University Press:
- 19 September 2018, pp. 629-635
-
- Article
-
- You have access
- Export citation
ON THE GROUP OF SEPARABLE QUADRATIC ALGEBRAS AND STACKS
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 151-167
-
- Article
-
- You have access
- Export citation
FOCAL SURFACES OF WAVE FRONTS IN THE EUCLIDEAN 3-SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2018, pp. 425-440
-
- Article
-
- You have access
- Export citation
EXISTENCE AND CONCENTRATION OF SOLUTION FOR A NON-LOCAL REGIONAL SCHRÖDINGER EQUATION WITH COMPETING POTENTIALS
-
- Published online by Cambridge University Press:
- 25 July 2018, pp. 441-460
-
- Article
-
- You have access
- Export citation
ON DEGENERATE SIGMA-FUNCTIONS IN GENUS 2
- Part of:
-
- Published online by Cambridge University Press:
- 25 June 2018, pp. 169-193
-
- Article
-
- You have access
- Export citation
CHARACTERIZING n-ISOCLINIC CLASSES OF CROSSED MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2018, pp. 637-656
-
- Article
-
- You have access
- Export citation
COMPLEX OF RELATIVELY HYPERBOLIC GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2018, pp. 657-672
-
- Article
-
- You have access
- Export citation
BONGARTZ τ-COMPLEMENTS OVER SPLIT-BY-NILPOTENT EXTENSIONS
-
- Published online by Cambridge University Press:
- 30 July 2018, pp. 461-470
-
- Article
-
- You have access
- Export citation
EXHAUSTION OF THE CURVE GRAPH VIA RIGID EXPANSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 06 July 2018, pp. 195-230
-
- Article
-
- You have access
- Export citation
ON IWASAWA THEORY OF RUBIN–STARK UNITS AND NARROW CLASS GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 31 October 2018, pp. 673-691
-
- Article
-
- You have access
- Export citation
FOURIER-TYPE TRANSFORMS ON REARRANGEMENT-INVARIANT QUASI-BANACH FUNCTION SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 231-248
-
- Article
-
- You have access
- Export citation
A PERTURBATION AND GENERIC SMOOTHNESS OF THE VAFA–WITTEN MODULI SPACES ON CLOSED SYMPLECTIC FOUR-MANIFOLDS
-
- Published online by Cambridge University Press:
- 13 July 2018, pp. 471-486
-
- Article
-
- You have access
- Export citation
Addendum
KOSZUL CALCULUS – ADDENDUM
-
- Published online by Cambridge University Press:
- 22 April 2018, p. 249
-
- Article
-
- You have access
- Export citation
Research Article
LUSTERNIK–SCHNIRELMANN CATEGORY BASED ON THE DISCRETE CONLEY INDEX THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 30 October 2018, pp. 693-704
-
- Article
-
- You have access
- Export citation
EXTREME POINTS FOR COMBINATORIAL BANACH SPACES
-
- Published online by Cambridge University Press:
- 27 July 2018, pp. 487-500
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 61 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 December 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation