Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T22:03:14.029Z Has data issue: false hasContentIssue false
  • English
  • Français

ON IWASAWA THEORY OF RUBIN–STARK UNITS AND NARROW CLASS GROUPS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  31 October 2018

YOUNESS MAZIGH
YOUNESS MAZIGH*
Affiliation:
Faculté des sciences de Meknès, Département de mathématiques, Université Moulay Ismail, B.P. 11201 Zitoune, Meknès 50000, Maroc e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a totally real number field of degree r. Let K∞ denote the cyclotomic 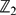-extension of K, and let L∞ be a finite extension of K∞, abelian over K. The goal of this paper is to compare the characteristic ideal of the χ-quotient of the projective limit of the narrow class groups to the χ-quotient of the projective limit of the rth exterior power of totally positive units modulo a subgroup of Rubin–Stark units, for some 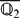$\overline{\mathbb{Q}_{2}}$-irreducible characters χ of Gal(L∞/K∞).

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11R29: Class numbers, class groups, discriminants 11R42: Zeta functions and $L$-functions of number fields
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 3 , September 2019 , pp. 673 - 691
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

Assim, J., Mazigh, Y. and Oukhaba, H., Théorie d’Iwasawa des unités de Stark et groupe de classes, Int. J. Number Theory 13 (5) (2017), 1165–1190.CrossRefGoogle Scholar
Assim, J. and Movahhedi, A., Galois codescent for motivic tame kernels. Submitted.Google Scholar
Bourbaki, N., Algébre commutative: Chapitres 5 á 7 (Springer Science & Business Media, Berlin, Germany, 2007).CrossRefGoogle Scholar
Büyükboduk, K., Stark units and the main conjectures for totally real fields, Compos. Math. 145 (5) (2009), 1163–1195.CrossRefGoogle Scholar
Chinburg, T., Kolster, M., V. Pappas and V. Snaith, Galois structure of K-groups of rings of integers, K-Theory 14 (1998), 319–369.CrossRefGoogle Scholar
Greither, C., Class groups of abelian fields, and the main conjecture, Ann. Inst. Fourier 42 (3) (1992), 449–499.CrossRefGoogle Scholar
Greither, C., On Chinburg’s second conjecture for abelian fields, J. R. Angew. Math. 479 (1996), 1–37.Google Scholar
Kahn, B., Descente galoisienne et K 2 des corps de nombres, K-Theory 7 (1993), 55–100.CrossRefGoogle Scholar
Mazigh, Y., Iwasawa theory of Rubin-Stark units and class groups, Manuscr. Math. 153 (3–4) (2017), 403–430.CrossRefGoogle Scholar
Mazur, B. and Rubin, K., Kolyvagin systems. Mem. Amer. Math. Soc. 168 (799) (2004), viii+96.Google Scholar
Mazur, B. and Rubin, K., Controlling Selmer groups in the higher core rank case, J. Théor. Nombres Bordeaux 28 (1) (2016), 145–183.CrossRefGoogle Scholar
Milne, J., Arithmetic duality theorems (Academic Press, Boston, 1986).Google Scholar
Nekovár, J., Selmer complexes, Astérisque 310 (2006), viii+559.Google Scholar
Oukhaba, H., On Iwasawa theory of elliptic units and 2-ideal class groups, J. Ramanujan Math. Soc. 27 (3) (2012), 255–227.Google Scholar
Perrin-Riou, B., Théorie d’Iwasawa et hauteurs p-adiques, Invent. Math. 109 (1992), 137–185.CrossRefGoogle Scholar
Rubin, K., A Stark conjecture “over ℤ” for abelian L-functions with multiple zeros, Ann. Inst. Fourier 46 (1) (1996), 33–62.CrossRefGoogle Scholar
Rubin, K., Euler systems, Annals of mathematics studies, 147. Hermann Weyl Lectures, The Institute for Advanced Study (Princeton University Press, Princeton).CrossRefGoogle Scholar
Tate, J., Les conjectures de Stark sur les fonctions L d’Artin en s = 0, in Progress in mathematics, vol. 47 (Lecture notes, Bernardi, D. and Schappacher, N., Editors) (Birkhäuser Basel, Basel, 1984).Google Scholar
Vauclair, D., Sur les normes universelles et la structure de certains modules d’Iwasawa (2006). Available at http://www.math.unicaen.fr/~vauclair/Google Scholar
Vauclair, D., Sur la dualité et la descente d’Iwasawa, Ann. Inst. Fourier 59 (2) (2009), 691–767.CrossRefGoogle Scholar