We call two measures equivalent if each is absolutely continuous with respect to the other (cf. [1]). Let G be a locally compact topological group and let μ be a non-negative Baire measure on G (i.e. μ is denned on all Baire sets, finite on compact sets and positive on open sets). We say that μ is stable if μ (E)=0 implies μ(tE)=0 for each t ∈ G. A. M. Macbeath made the conjecture that every stable non-trivial Baire measure is equivalent to the Haar measure. In this paper we prove the following slightly stronger result:

Theorem. Every stable non-trivial measure defined on Baire sets and finite on some open set is equivalent to the Haar measure.

Hurwitz's theorem says that the limit of schlicht functions, in the topology of compact convergence, is again a schlicht function or a constant function. We generalize this to mappings between Riemann surfaces and get more precise information on the relation between the distribution of values of analytic functions and the topology of compact convergence on the space of all analytic maps.

All operators considered in this paper are bounded and linear (everywhere defined) on a Hilbert space. An operator A will be called a square root of an operator B if

A simple sufficient condition guaranteeing that any solution A of (1) be normal whenever B is normal was obtained in [1], namely: If B is normal and if there exists some real angle θ for which Re(Aeιθ)≥0, then (1) implies that A is normal. Here, Re (C) denotes the real part ½(C + C*) of an operator C.

In a recent joint paper with J. C. Cooke [1], we have given a method of determining the coefficients an in the “dual” Fourier-Bessel series

where −1 ≤p≤, F(r) is specified and αn is a positive root of Jv(αnα) = 0. This method reduced the problem to the solution of an infinite set of algebraical equations and it was shown that, under certain circumstances, numerical values for the coefficients could be obtained fairly readily.

In a recent paper [1], the author divided the semi-special permutations on [n] that are not linear into two classes. The first class consists of the semi-special permutations which, for all possible values of s, have s as a principal number and which induce modulo s the identity permutation. The second class consists of all the semi-special permutations, with principal number s, which induce modulo s linear permutations other than the identity, where again s takes all its possible values.

Three different sets of equations connecting the sums of angles in an n-dimensional simplex have been given by Sommerville [7], Höhn [5], and Peschl [6]. The equivalence of the first two sets of equations has been proved by Sprott [7].

In the present note it is shown that results are simplified if we consider averages instead of sums, and that the averages form a sequence which is self-reciprocal with respect to the transformation

The equivalence of the sets of equations is then easily proved by symbolic methods.

1. All operators considered in this paper are bounded operators on a Hilbert space. In case A and B are self-adjoint, certain conditions on A, B and their difference

assuring the unitary equivalence of Aand B,

have recently been obtained by Rosenblum [6] and Kato [2]. The present paper will consider the problem of investigating consequences of an assumed relation of type (2) for some unitary U together with an additional hypothesis that the difference H of (1) be non-negative, so that

First, it is easy to see that if only (2) and (3) are assumed, thereby allowing H = 0, relation (2) can hold for A arbitrary with U = I (identity) and B = A. If H = 0 in (3) is not allowed, however (an impossible assumption in the finite dimensional case, incidentally, since then the trace of H is zero and hence H = 0), it will be shown, among other things, that any unitary operator U for which (2) and (3) hold must have a spectrum with a positive measure (as a consequence of (i) of Theorem 2 below). Moreover A (hence B) cannot differ from a completely continuous operator by a constant multiple of the identity (Theorem 1). In case 0 is not in the point spectrum of H, then U is even absolutely continuous (see (iv) of Theorem 2). In § 4, applications to semi-normal operators will be given.

The existence of a function g of hhaving the property that pr divides the order of the automorphism group of a finite group G whenever pg divides the order of G was first established by Ledermann and Neumann [4], who showed that the least such function g(h) satisfies the inequality

Later Green [2] improved this estimate to

In the Present paper this will be revised, for sufficiently large h, to

Let G be a given group and A, B be two subgroups of G which may or may not coincide. A homomorphism μ which maps A onto B is called a partial endomorphism of G. When A coincides with G then we call μ a total endomorphism or as it is usually called an endomorphism of G. If μ* is a partial (or total) endomorphism of a supergroup G* ⊇ G, then we say that μ* extends, or continues, μ when μ* is defined for at least all the elements a ∈ A and moreover aμ = aμ* for all a ∈ A If the partial endomorphism μ is an isomorphic mapping then we speak of a partial automorphism of G.

When the theory of Hankel transforms is applied to the solution of certain mixed boundary value problems in mathematical physics, the problems are reduced to the solution of dual integral equations of the type

where α and ν are prescribed constants and f(ρ) is a prescribed function of ρ [1]. The formal solution of these equations was first derived by Titchmarsh [2]. The method employed by Titchmarsh in deriving the solution in the general case is difficult, involving the theory of Mellin transforms and what is essentially a Wiener-Hopf procedure. In lecturing to students on this subject one often feels the need for an elementary solution of these equations, especially in the cases α = ± 1, ν = 0. That such an elementary solution exists is suggested by Copson's solution [3] of the problem of the electrified disc which corresponds to the case α = –l, ν = 0. A systematic use of a procedure similar to Copson's has in fact been made by Noble [4] to find the solution of a pair of general dual integral equations, but again the analysis is involved and long. The object of the present note is to give a simple solution of the pairs of equations which arise most frequently in physical applications. The method of solution was suggested by a procedure used by Lebedev and Uflyand [5] in the solution of a much more general problem.

In the course of some recent work on Fourier series [5, 6] I had occasion to use a number of integral inequalities which were generalizations or limiting cases of known results. These inequalities may perhaps have other applications, and it seems worth while to collect them together in a separate note with one or two further results of a similar nature.

For any number k, used as an index (exponent), and such that K > 1, we write k' = k′(k–1), so that k and k′ are conjugate indices in the sense of Hölder's inequality.

To what extent is the structure of a Lie-algebra L over a field F determined by the bilinear form

on L that is derived from a matrix representation

of L with finite degree d(Δ) by forming the trace of the matrix products

Such a bilinear form is a function with two arguments in L, values in F and the properties:

The following work establishes a new proof of the theorem: Every archimedean ordered group is abelian. This theorem has been proved differently by many authors. It was first proved by O. Hölder [2]. A second proof has been given by H. Cartan [1]: he uses the topology which is naturally introduced in the group by its order.

Let

be a positive definite quadratic form with determinant αβ−X2 = 1. A special form of this kind is

We consider the Epstein zeta-function

the series converging for s > 1. For s ≥ 1·035 Rankin [1] proved the following

STatement R.

The sign of equality is needed only when h is equivalent to Q.

In this paper we evaluate some integrals involving U-functions by the methods of the Operational Calculus. The results obtained are quite general and many of them include, as particular cases, some known results.

A function ψ (p) is operationally related with another function f(t), if they satisfy the integral equation

2. Theorem. If

and

As usual, we shall denote (1) by the symbolic expression

provided that the integral is convergent. HereR(α) > 0, R(p) > 0, n = 2,3,4, …, andmeans that in the expression following it, i is to bee replaced by – i and the two expressions are to be added.

Let L = L( +, v, ＾) be a lattice-ordered group, or l-group (Birkhoff [1, p. 214]). Two elements a and b of L will be called disjoint if a > 0, b > 0, and a ＾; b = 0. It is easily seen that if L does not contain two disjoint elements, then it is linearly ordered (and, of course, conversely). What can we say about Z-groups containing two but not more than two mutually disjoint elements?

Let Aand B be linearly ordered groups (o-groups), and let A ⋏ B be the cardinal sum of A and B. That is, A ⋏ B is the direct sum of A and B, and (a, b) is positive in A + B if and only if a is positive in A and b is positive in B. An l-group L containing A ⋏ B as a convex normal subgroup (or Z-ideal) is called a lexico-extension of A ⋏ B if every positive element of L not in A ⋏ B exceeds every element of A ⋏ B. It then follows (subsection 2.9 below) that L/(A ⋏ B) is an o-group. Such an l-group L is easily seen to satisfy the following condition: (D)

There exists a pair of disjoint elements in L, but no triple of pairwise disjoint elements exists in L.

In this paper three integrals involving E-functions are evaluated in terms of E-functions. The formulae to be established are:

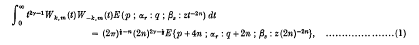
where n is a positive integer, | args z < π, R(γ ± m ÷ ½) > 0, αρ+ν = (2γ + ν)/2n (ν = 1, 2, …, 2n), αρ+2n+i = (γ + m - ½ + i)/n, αρ+3n+i = (γ - m - ½ + i)/n, βα+i = (γ + κ + i)/n, βα+ν+i = (γ - κ + i)/n(i = 1, 2, …, n).

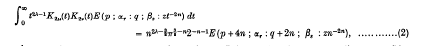
where n is a positive integer, |arg z| < π, R(λ±μ±ν) > 0, αp+i+1 = (λ + μ + ν + i)/n, αp+n+i+1 = (λ - μ + ν + i)/n, αp+2n+i+1 = (λ + μ - ν + i)/n, αp+3n+i+1 = (λ - μ - ν + i)/n (i = 0, 1, 2, …, n - 1), βa+i+1 = (2λ + j)/2n (j = 0, 1, 2, …, 2n - 1).

where n is a positive integer, R(λ) > ½, |arg z| < π, αp+i+1 = (2λ - 1 + i)/2n (i = 0, 1, 2, …, 2n-1), βq+j+1 = (λ + μ j)/n, βq+n+j+1 = (λ - μ + j)/n (j = 0, 1, 2, …, n-1).

be a given series and let

With Flett [4], we say that the series is summable , q real, if

where Summability |C, k, 0|1 is identical with absolute Cesàro summability (C, k), or summability |C, k|, as defined by Fekete [3].

A point x in the real or complex space lpis an infinite sequence,(x1, x2, x3,…) of real or complex numbers such that is convergent. Here p ≥ 1 and we write

The unit sphere S consists of all points x ε lp for which ¶ x ¶ ≤ 1. The sphere of radius a≥ ≤ 0 and centre y is denoted by Sa(y) and consists of all points x ε lp such that ¶ x - y ¶ ≤ a. The sphere Sa(y) is contained in S if and only if ¶ y ¶≤1 - a, and the two spheres Sa(y) and Sa(z) do not overlap if and only if

¶ y- z ¶≥ 2a

The statement that a finite or infinite number of spheres Sa (y) of fixed radius a can be packed in S means that each sphere Sa (y) is contained in S and that no two such spheres overlap.

In two recent papers [1, 2] the Barnes integral for the E-functions was employed to sum a number of infinite series of E-functions. In §2 of this paper, by making use of the multiplication formula for the gamma function, the method is extended to series of E-functions of a different type.