Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T07:44:51.958Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Integrals Involving E-Functions

Published online by Cambridge University Press:  18 May 2009

R. K. Saxena
R. K. Saxena
Affiliation:
Maharana Bhupal College, Udaipur
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we evaluate some integrals involving U-functions by the methods of the Operational Calculus. The results obtained are quite general and many of them include, as particular cases, some known results.

A function ψ (p) is operationally related with another function f(t), if they satisfy the integral equation

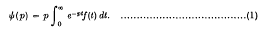
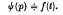
2. Theorem. If

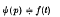
and

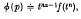
As usual, we shall denote (1) by the symbolic expression

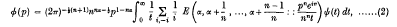
provided that the integral is convergent. HereR(α) > 0, R(p) > 0, n = 2,3,4, …, and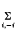means that in the expression following it, i is to bee replaced by – i and the two expressions are to be added.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 4 , Issue 4 , September 1960 , pp. 178 - 185
Copyright
Copyright © Glasgow Mathematical Journal Trust 1960

References

1.Erdélyi, A., Tables of integral transforms, Vol. I (New York, 1954).Google Scholar
2.Goldstein, S., Operational representation of Whittaker's confluent hypergeometric function and Weber's parabolic cylinder functions, Proc. London Math. Soc., (2) 34 (1932), 103–125.CrossRefGoogle Scholar
3.Shanker, Hari, Some definite integrals involving confluent hypergeometric functions, J. London Math. Soc., 23 (1948), 44–49.CrossRefGoogle Scholar
4.MacRobert, T. M., Functions of a complex variable (London, 1954).Google Scholar
5.MacRobert, T. M., Integrals allied to Airy's integrals, Proc. Glasgow Math. Assoc., 3 (1957), 91–93.Google Scholar
6.Ragab, F. M., Integrals involving E-functions and Bessel functions, Koninkl. Nederl. Akademie van Wetenschappen, Amsterdam, 57 (1954), 414–423.Google Scholar
7.Ragab, F. M., The inverse Laplace transform of an exponential function, Communications on Pure and Applied Mathematics (New York University), 11 (1958), 115–127.Google Scholar
8.Rathie, C. B., Some infinite integrals involving E-functions, J. Indian Math. Soc., (4), 17 (1953), 167–175.Google Scholar
9.Rathie, C. B., Some results involving hypergeometric and E-functions, Proc. Glasgow Math. Assoc., 2 (1955), 132–138.CrossRefGoogle Scholar
10.Rathie, C. B., A few infinite integrals involving E-functions, Proc. Glasgow Math. Assoc., 2 (1956), 170–172.CrossRefGoogle Scholar
11.Sharma, K. C., Infinite integrals involving products of Legendre functions, Proc. Glasgow Math. Assoc., 3 (1957), 111–118.CrossRefGoogle Scholar
12.Sharma, K. C., Infinite integrals involving E-functions, Proc. Nat. Inst. Sci., India, 25 (1959), 161–165.Google Scholar