Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T07:51:49.504Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Angles in an n-Dimensional Simplex

Published online by Cambridge University Press:  18 May 2009

A. P. Guinand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Three different sets of equations connecting the sums of angles in an n-dimensional simplex have been given by Sommerville [7], Höhn [5], and Peschl [6]. The equivalence of the first two sets of equations has been proved by Sprott [7].

In the present note it is shown that results are simplified if we consider averages instead of sums, and that the averages form a sequence which is self-reciprocal with respect to the transformation

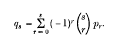
The equivalence of the sets of equations is then easily proved by symbolic methods.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 4 , Issue 2 , July 1959 , pp. 58 - 61
Copyright
Copyright © Glasgow Mathematical Journal Trust 1959

References

1.Barrucand, P., Sur les suites reciproques, Comptes Bendus, 230 (1950), 1727–8.Google Scholar
2.Coxeter, H. S. M., Math. Reviews, 15 (1954), 55, and 18 (1957), 55.Google Scholar
3.Guinand, A. P, Matrices associated with fractional Hankel and Fourier transforms, Proc. Glasgow Math. Assoc. 2 (1956), 185–92.CrossRefGoogle Scholar
4.Hardy, G. H., Divergent series (Oxford, 1949), 247.Google Scholar
5.Höhn, W., Winkel and Winkelsumme im n-dimensionalen euklidischen Simplex, Thesis, Eidgenössische Technische Hochschule (Zürich, 1953).Google Scholar
6.Peschl, E., Winkelrelationen am Simplex und die Eulersche Charakteristik, Bayer. Akad. Wiss. Math.-Nat. Kl. S.-B., 1955, 319–45.Google Scholar
7.Sommerville, D. M. Y., The relations connecting the angle-sums and volume of a polytope in space of n dimensions, Proc. Roy. Soc. London, A 115 (1927), 103–19.Google Scholar
8.Sprott, D. A., A combinatorial identity, Math. Gazette, 40 (1956), 207–9.CrossRefGoogle Scholar