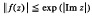Research Article
A characterization of the definiteness of a Hermitian matrix
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-4
-
- Article
-
- You have access
- Export citation
The stability of pure weights under conditioning
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 5-12
-
- Article
-
- You have access
- Export citation
Order and norm convergence in Banach lattices
-
- Published online by Cambridge University Press:
- 18 May 2009, p. 13
-
- Article
-
- You have access
- Export citation
Partitioned transversals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 14-16
-
- Article
-
- You have access
- Export citation
Hecke invariants of knot groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 17-26
-
- Article
-
- You have access
- Export citation
A local mean-value theorem for analytic functions with smooth boundary values
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 27-29
-
- Article
-
- You have access
- Export citation
Quasi-homology and universal coefficients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 30-38
-
- Article
-
- You have access
- Export citation
Semigroups of non-negative integral matrices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-42
-
- Article
-
- You have access
- Export citation
A note on uniqueness for anisotropic fluids
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 43-47
-
- Article
-
- You have access
- Export citation
An approximative property of spaces of continuous functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 48-53
-
- Article
-
- You have access
- Export citation
On commutative non-self-adjoint operator algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 54-59
-
- Article
-
- You have access
- Export citation
A characterization of determinants over topological fields
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 60-62
-
- Article
-
- You have access
- Export citation
Axiomatisations of the average and a further generalisation of monotonic sequences
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-65
-
- Article
-
- You have access
- Export citation
Delange's characterization of the sine function
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 66-68
-
- Article
-
- You have access
- Export citation
Asymmetric and symmetric graphs
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 69-73
-
- Article
-
- You have access
- Export citation
A generalization of Clifford algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 74-78
-
- Article
-
- You have access
- Export citation
Chain conditions on posets
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 79-81
-
- Article
-
- You have access
- Export citation
The convergence of least squares approximations for dual orthogonal series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 82-84
-
- Article
-
- You have access
- Export citation
Semi-algebras in C(T)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 85-87
-
- Article
-
- You have access
- Export citation
On a conjecture of G. Hajós
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 88-89
-
- Article
-
- You have access
- Export citation

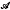 of nonempty sets satisfying certain conditions (irredundancy and coherence) and we called such sets
of nonempty sets satisfying certain conditions (irredundancy and coherence) and we called such sets 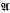 = (A
= (A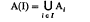

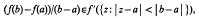
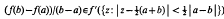
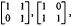 , and every other non-unit is expressible uniquely as products of these primes. Before formally stating this result, we need some notation. Let
, and every other non-unit is expressible uniquely as products of these primes. Before formally stating this result, we need some notation. Let 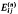 the
the 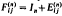 . When the dimension is clear, we shall drop the superscripts.
. When the dimension is clear, we shall drop the superscripts.