Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-27T06:29:55.537Z Has data issue: false hasContentIssue false
  • English
  • Français

The stability of pure weights under conditioning

Published online by Cambridge University Press:  18 May 2009

D. J. Foulis  and
C. H. Randall
D. J. Foulis
Affiliation:
University of Massachusetts, Amherst, Mass. 01002
C. H. Randall
Affiliation:
University of Massachusetts, Amherst, Mass. 01002
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1], we showed how a collection of physical operations or experiments could be represented by a nonempty set 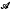of nonempty sets satisfying certain conditions (irredundancy and coherence) and we called such sets 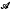. We also introduced “complete stochastic models” for the empirical universe of discourse represented by such a manual 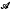, namely, the so-called weight functions for 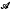. These weight functions form a convex set the extreme points of which are called pure weights. We also showed that there is a so-called logic ∏(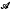) affiliated with a manual 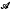and that each weight function for 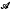induces a state on this logic.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 15 , Issue 1 , March 1974 , pp. 5 - 12
Copyright
Copyright © Glasgow Mathematical Journal Trust 1974

References

REFERENCES

1.Foulis, D. and Randall, C., Operational statistics I, basic concepts, J. Mathematical Physics 13 (1972), 1667–1675.Google Scholar
2.Foulis, D. and Randall, C., Conditioning maps on orthomodular lattices, Glasgow Math. J. 12 (1971), 35–42.Google Scholar
3.Greechie, R., Orthomodular lattices admitting no states,J. Combinatorial Theory 10 (1971), 119–132.CrossRefGoogle Scholar
4.Greechie, R. and Miller, F., On structures related to states on an empirical logic: I. Weights on finite spaces, Kansas State University mimeographed notes, 1969.Google Scholar
5.Lüders, G., Über die Zustandsänderung durch den Messprozess, Ann. Physik 8 (1951), 322–328.Google Scholar
6.Messiah, A., Quantum Mechanics. Vol. 1 (Amsterdam, 1961).Google Scholar
7.Pool, J., Semimodularity and the logic of quantum mechanics, Comm. Math. Phys. 9 (1968), 212–228.Google Scholar
8.Randall, C. and Foulis, D., An approach to empirical logic, Amer. Math. Monthly 77 (1970), 363–374.CrossRefGoogle Scholar
9.Randall, C. and Foulis, D., States and the free orthogonality monoid, Math. Systems Theory 6 (1972), 268–276.Google Scholar