No CrossRef data available.
Article contents
Semigroups of non-negative integral matrices
Published online by Cambridge University Press: 18 May 2009
Extract
In [1], Pall proved an interesting result on a certain class of 2 × 2 integral matrices. He showed that the semigroup of 2 × 2 matrices of determinant 1 and non-negative entries contains exactly 2 primes 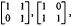 , and every other non-unit is expressible uniquely as products of these primes. Before formally stating this result, we need some notation. Let Gn denote the semigroup of n × n matrices with determinant 1 and nonnegative integral entries, In the n × n identity matrix,
, and every other non-unit is expressible uniquely as products of these primes. Before formally stating this result, we need some notation. Let Gn denote the semigroup of n × n matrices with determinant 1 and nonnegative integral entries, In the n × n identity matrix, 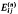 the n × n matrix with a 1 as its (i, j) element and zeros elsewhere, and let
the n × n matrix with a 1 as its (i, j) element and zeros elsewhere, and let 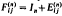 . When the dimension is clear, we shall drop the superscripts.
. When the dimension is clear, we shall drop the superscripts.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1974


