Let 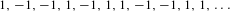 $1,-1,-1,1,-1,1,1,-1,-1,1,1,\ldots$ be the
$1,-1,-1,1,-1,1,1,-1,-1,1,1,\ldots$ be the 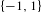 $\{-1,1\}$-valued Thue–Morse sequence. Its correlation dimension is
$\{-1,1\}$-valued Thue–Morse sequence. Its correlation dimension is 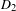 $D_{2}$, satisfying
$D_{2}$, satisfying 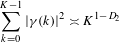 $$\begin{eqnarray}\mathop{\sum }_{k=0}^{K-1}|{\it\gamma}(k)|^{2}\asymp K^{1-D_{2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=0}^{K-1}|{\it\gamma}(k)|^{2}\asymp K^{1-D_{2}}\end{eqnarray}$$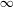 $\infty$ as
$\infty$ as 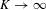 $K\rightarrow \infty$, where
$K\rightarrow \infty$, where 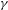 ${\it\gamma}$ is the correlation function; its value is known [Zaks, Pikovsky and Kurths. On the correlation dimension of the spectral measure for the Thue–Morse sequence. J. Stat. Phys.88(5/6) (1997), 1387–1392] to be
${\it\gamma}$ is the correlation function; its value is known [Zaks, Pikovsky and Kurths. On the correlation dimension of the spectral measure for the Thue–Morse sequence. J. Stat. Phys.88(5/6) (1997), 1387–1392] to be 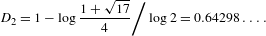 $$\begin{eqnarray}D_{2}=1-\log \frac{1+\sqrt{17}}{4}\bigg/\log 2=0.64298\ldots .\end{eqnarray}$$
$$\begin{eqnarray}D_{2}=1-\log \frac{1+\sqrt{17}}{4}\bigg/\log 2=0.64298\ldots .\end{eqnarray}$$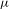 ${\it\mu}$ on
${\it\mu}$ on 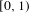 $[0,1)$, consider the transformation
$[0,1)$, consider the transformation  $T$ with
$T$ with 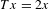 $Tx=2x$ (
$Tx=2x$ (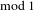 $\text{mod}~1$). It is shown to be of Kolmogorov type having entropy at least
$\text{mod}~1$). It is shown to be of Kolmogorov type having entropy at least 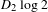 $D_{2}\log 2$. Moreover, a random walk is defined by
$D_{2}\log 2$. Moreover, a random walk is defined by 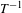 $T^{-1}$ which has the transition probability
$T^{-1}$ which has the transition probability 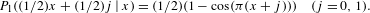 $$\begin{eqnarray}P_{1}((1/2)x+(1/2)j\mid x)=(1/2)(1-\cos ({\it\pi}(x+j)))\quad (j=0,1).\end{eqnarray}$$
$$\begin{eqnarray}P_{1}((1/2)x+(1/2)j\mid x)=(1/2)(1-\cos ({\it\pi}(x+j)))\quad (j=0,1).\end{eqnarray}$$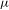 ${\it\mu}$ is the unique stationary measure. Moreover,
${\it\mu}$ is the unique stationary measure. Moreover, 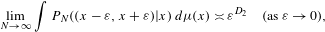 $$\begin{eqnarray}\lim _{N\rightarrow \infty }\int P_{N}((x-{\it\varepsilon},x+{\it\varepsilon})|x)\,d{\it\mu}(x)\asymp {\it\varepsilon}^{D_{2}}\quad (\text{as}~{\it\varepsilon}\rightarrow 0),\end{eqnarray}$$
$$\begin{eqnarray}\lim _{N\rightarrow \infty }\int P_{N}((x-{\it\varepsilon},x+{\it\varepsilon})|x)\,d{\it\mu}(x)\asymp {\it\varepsilon}^{D_{2}}\quad (\text{as}~{\it\varepsilon}\rightarrow 0),\end{eqnarray}$$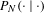 $P_{N}(\cdot \mid \cdot )$ is the
$P_{N}(\cdot \mid \cdot )$ is the 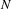 $N$-step transition probability.
$N$-step transition probability.