Spectral measure of the Thue–Morse sequence and the dynamical system and random walk related to it

Abstract

Let 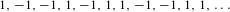$1,-1,-1,1,-1,1,1,-1,-1,1,1,\ldots$ be the 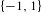$\{-1,1\}$-valued Thue–Morse sequence. Its correlation dimension is 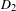$D_{2}$, satisfying

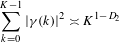$$\begin{eqnarray}\mathop{\sum }_{k=0}^{K-1}|{\it\gamma}(k)|^{2}\asymp K^{1-D_{2}}\end{eqnarray}$$

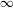in the sense that the ratio between the left- and right-hand sides is bounded away from 0 and $\infty$ as 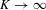$K\rightarrow \infty$, where 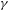${\it\gamma}$ is the correlation function; its value is known [Zaks, Pikovsky and Kurths. On the correlation dimension of the spectral measure for the Thue–Morse sequence. J. Stat. Phys.88(5/6) (1997), 1387–1392] to be

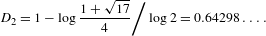$$\begin{eqnarray}D_{2}=1-\log \frac{1+\sqrt{17}}{4}\bigg/\log 2=0.64298\ldots .\end{eqnarray}$$

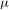Under its spectral measure ${\it\mu}$ on 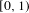$[0,1)$, consider the transformation $T$ with 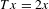$Tx=2x$ (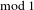$\text{mod}~1$). It is shown to be of Kolmogorov type having entropy at least 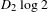$D_{2}\log 2$. Moreover, a random walk is defined by 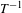$T^{-1}$ which has the transition probability

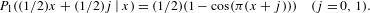$$\begin{eqnarray}P_{1}((1/2)x+(1/2)j\mid x)=(1/2)(1-\cos ({\it\pi}(x+j)))\quad (j=0,1).\end{eqnarray}$$

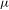It is proved that this random walk is mixing and ${\it\mu}$ is the unique stationary measure. Moreover,

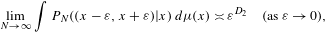$$\begin{eqnarray}\lim _{N\rightarrow \infty }\int P_{N}((x-{\it\varepsilon},x+{\it\varepsilon})|x)\,d{\it\mu}(x)\asymp {\it\varepsilon}^{D_{2}}\quad (\text{as}~{\it\varepsilon}\rightarrow 0),\end{eqnarray}$$

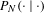where $P_{N}(\cdot \mid \cdot )$ is the 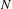$N$-step transition probability.