Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T20:46:51.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence groups and semiconjugacy

Published online by Cambridge University Press:  10 November 2014

DANIEL MONCLAIR
DANIEL MONCLAIR*
Affiliation:
UMPA, École Normale Supérieure de Lyon, 46 allée d’Italie, 69364 Lyon Cedex 07, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a problem that arises from the study of Lorentz surfaces and Anosov flows. For a non-decreasing map of degree one 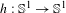$h:\mathbb{S}^{1}\rightarrow \mathbb{S}^{1}$, we are interested in groups of circle diffeomorphisms that act on the complement of the graph of 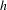$h$ in 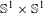$\mathbb{S}^{1}\times \mathbb{S}^{1}$ by preserving a volume form. We show that such groups are semiconjugate to subgroups of 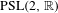$\text{PSL}(2,\mathbb{R})$ and that, when 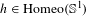$h\in \text{Homeo}(\mathbb{S}^{1})$, we have a topological conjugacy. We also construct examples where 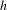$h$ is not continuous, for which there is no such conjugacy.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1221 - 1246
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlfors, L. V.. Finitely generated Kleinian groups. Amer. J. Math. 86 (1964), 413–429.Google Scholar
Barbot, T.. Caractérisation des flots d’Anosov en dimension 3 par leurs feuilletages faibles. Ergod. Th. & Dynam. Sys. 15(2) (1995), 247–270.CrossRefGoogle Scholar
Barbot, T.. Flots d’Anosov sur les variétés graphées au sens de Waldhausen. Ann. Inst. Fourier (Grenoble) 46 (1996), 1451–1517.CrossRefGoogle Scholar
Barbot, T.. Plane affine geometry of Anosov flows. Ann. Sci. Éc. Norm. Supér. (4) 34(6) (2001), 871–889.Google Scholar
Bers, L.. Automorphic forms and Poincaré series for infinitely generated Fuchsian groups. Amer. J. Math. 87 (1965), 196–214.Google Scholar
Button, J.. Matrix representations and the Teichmüller space of the twice punctured torus. Conform. Geom. Dyn. 4 (2000), 97–107.Google Scholar
Casson, A. and Jungreis, D.. Convergence groups and Seifert fibered 3-manifolds. Invent. Math. 118(3) (1994), 441–456.Google Scholar
Denjoy, A.. Sur les courbes définies par les équations différentielles à la surface du tore. J. Math. Pures Appl. (9) 11 (1932), 333–375.Google Scholar
Foulon, P. and Hasselblatt, B.. Contact Anosov flows on hyperbolic 3-manifolds. Geom. Topol. 17 (2013), 1225–1252.Google Scholar
Gabai, D.. Convergence groups are Fuchsian groups. Ann. of Math. (2) 136 (1992), 447–510.Google Scholar
Ghys, E.. Flots d’Anosov dont les feuilletages stables sont différentiables. Ann. Sci. Éc. Norm. Supér. (4) 20(2) (1987), 251–270.Google Scholar
Ghys, E.. Groupes d’homéomorphismes du cercle et cohomologie bornée. Contemp. Math. 58(Part III) (1987), 81–106.Google Scholar
Ghys, E.. Déformations de flots d’Anosov et de groupes fuchsiens. Ann. Inst. Fourier (Grenoble) 42 (1992), 209–247.Google Scholar
Ghys, E.. Rigidité différentiable des groupes fuchsiens. Publ. Math. Inst. Hautes Études Sci. 78 (1993), 163–185.Google Scholar
Ghys, E.. Groups acting on the circle. Enseign. Math. (2) 47(3–4) (2001), 329–407.Google Scholar
Herman, M. R.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–234.Google Scholar
Hirsh, M. and Pugh, C.. Stable manifolds for hyperbolic sets. Bull. Amer. Math. Soc. 75(1) (1969), 149–152.Google Scholar
Hurder, S. and Katok, A.. Differentiability, rigidity, and Godbillon–Vey classes for Anosov flows. Publ. Math. Inst. Hautes Études Sci. 72 (1990), 5–61.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Livšic, A. N.. Homology properties of U systems. Math. Notes 10 (1971), 758–763.Google Scholar
Matsumoto, S.. Some remarks on foliated S 1 bundles. Invent. Math. 90 (1987), 343–358.Google Scholar
Monclair, D.. Differential conjugacy for groups of area preserving circle diffeomorphisms. Preprint, 2014, arXiv:1402.0424.Google Scholar
Monclair, D.. Convergence groups and semi conjugacy. Preprint, 2014, arXiv:1402.7179.Google Scholar
Monclair, D.. Dynamique lorentzienne et groupes de difféomorphismes du cercle. PhD Thesis, Ecole Normale Supérieure de Lyon, 2014.Google Scholar
Navas, A.. Reduction of cocycles and groups of diffeomorphisms of the circle. Bull. Belg. Math. Soc. 13 (2006), 193–205.Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 2011.Google Scholar