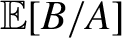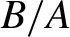ARTICLES
CHARACTERIZATION OF THE TAIL BEHAVIOR OF A CLASS OF BEKK PROCESSES: A STOCHASTIC RECURRENCE EQUATION APPROACH
-
- Published online by Cambridge University Press:
- 04 February 2021, pp. 1-34
-
- Article
- Export citation
GENERALIZED LAPLACE INFERENCE IN MULTIPLE CHANGE-POINTS MODELS
-
- Published online by Cambridge University Press:
- 23 February 2021, pp. 35-65
-
- Article
- Export citation
ESTIMATION AND INFERENCE FOR MOMENTS OF RATIOS WITH ROBUSTNESS AGAINST LARGE TRIMMING BIAS
-
- Published online by Cambridge University Press:
- 23 February 2021, pp. 66-112
-
- Article
- Export citation
UNIT ROOT TEST WITH HIGH-FREQUENCY DATA
-
- Published online by Cambridge University Press:
- 08 April 2021, pp. 113-171
-
- Article
-
- You have access
- Open access
- Export citation
MISCELLANEA
ON THE UNIFORM CONVERGENCE OF DECONVOLUTION ESTIMATORS FROM REPEATED MEASUREMENTS
-
- Published online by Cambridge University Press:
- 25 January 2021, pp. 172-193
-
- Article
- Export citation
ON SMOOTH TESTS FOR THE EQUALITY OF DISTRIBUTIONS
-
- Published online by Cambridge University Press:
- 12 January 2021, pp. 194-208
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ECT volume 38 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 February 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ECT volume 38 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 February 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation