Article contents
ESTIMATION AND INFERENCE FOR MOMENTS OF RATIOS WITH ROBUSTNESS AGAINST LARGE TRIMMING BIAS
Published online by Cambridge University Press: 23 February 2021
Abstract
Researchers often trim observations with small values of the denominator A when they estimate moments of the form
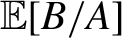 $\mathbb {E}[B/A]$
. Large trimming is common in practice to reduce variance, but it incurs a large bias. This paper provides a novel method of correcting the large trimming bias. If a researcher is willing to assume that the joint distribution between A and B is smooth, then the trimming bias may be estimated well. Along with the proposed bias correction method, we also develop an inference method. Practical advantages of the proposed method are demonstrated through simulation studies, where the data generating process entails a heavy-tailed distribution of
$\mathbb {E}[B/A]$
. Large trimming is common in practice to reduce variance, but it incurs a large bias. This paper provides a novel method of correcting the large trimming bias. If a researcher is willing to assume that the joint distribution between A and B is smooth, then the trimming bias may be estimated well. Along with the proposed bias correction method, we also develop an inference method. Practical advantages of the proposed method are demonstrated through simulation studies, where the data generating process entails a heavy-tailed distribution of
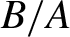 $B/A$
. Applying the proposed method to the Compustat database, we analyze the history of external financial dependence of U.S. manufacturing firms for years 2000–2010.
$B/A$
. Applying the proposed method to the Compustat database, we analyze the history of external financial dependence of U.S. manufacturing firms for years 2000–2010.
- Type
- ARTICLES
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
First arXiv date: 4 September 2017 (arXiv:1709.00981). We benefited from useful comments by Peter C. B. Phillips (editor), Arthur Lewbel (co-editor), anonymous referees, numerous researchers, seminar participants at Australian National University, University of Bristol, University of British Columbia, Chinese University of Hong Kong, Duke University, Emory University, Fudan University, Hong Kong University of Science and Technology, University of Melbourne, Monash University, Northwestern University, University of Sydney, University of California Davis, University of California San Diego, University of New South Wales, and University of Technology Sydney, and conference participants at 2018 Asian Meeting of the Econometric Society, 2018 Cemmap Advances in Econometrics, 2018 China Meeting of the Econometric Society, 2019 Asian Meeting of the Econometric Society, 2018 International Association for Applied Econometrics Annual Conference, and New York Camp Econometrics XIII. All remaining errors are ours.
References
REFERENCES
- 11
- Cited by


