Published online by Cambridge University Press: 04 February 2021
We consider conditions for strict stationarity and ergodicity of a class of multivariate BEKK processes
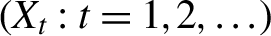 $(X_t : t=1,2,\ldots )$
and study the tail behavior of the associated stationary distributions. Specifically, we consider a class of BEKK-ARCH processes where the innovations are assumed to be Gaussian and a finite number of lagged
$(X_t : t=1,2,\ldots )$
and study the tail behavior of the associated stationary distributions. Specifically, we consider a class of BEKK-ARCH processes where the innovations are assumed to be Gaussian and a finite number of lagged
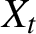 $X_t$
’s may load into the conditional covariance matrix of
$X_t$
’s may load into the conditional covariance matrix of
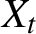 $X_t$
. By exploiting that the processes have multivariate stochastic recurrence equation representations, we show the existence of strictly stationary solutions under mild conditions, where only a fractional moment of
$X_t$
. By exploiting that the processes have multivariate stochastic recurrence equation representations, we show the existence of strictly stationary solutions under mild conditions, where only a fractional moment of
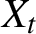 $X_t$
may be finite. Moreover, we show that each component of the BEKK processes is regularly varying with some tail index. In general, the tail index differs along the components, which contrasts with most of the existing literature on the tail behavior of multivariate GARCH processes. Lastly, in an empirical illustration of our theoretical results, we quantify the model-implied tail index of the daily returns on two cryptocurrencies.
$X_t$
may be finite. Moreover, we show that each component of the BEKK processes is regularly varying with some tail index. In general, the tail index differs along the components, which contrasts with most of the existing literature on the tail behavior of multivariate GARCH processes. Lastly, in an empirical illustration of our theoretical results, we quantify the model-implied tail index of the daily returns on two cryptocurrencies.
We thank Peter C.B. Phillips (editor), Robert Taylor (co-editor), and two referees for helpful comments and suggestions that have led to a much improved paper. Moreover, we thank Ewa Damek, Rustam Ibragimov, Anders Rahbek, and participants at the 2019 CFE Conference for valuable suggestions. Matsui’s research is partly supported by the JSPS Grant-in-Aid for Young Scientists B (16k16023) and for Scientific Research C (19K11868). Pedersen is grateful for support from the Carlsberg Foundation (CF16-0909, ”Robust methods for volatility modelling”).