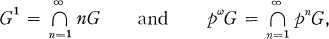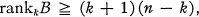Research Article
On a Generalization of Alternative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 953-966
-
- Article
-
- You have access
- Export citation
Reconstruction of Trees
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-60
-
- Article
-
- You have access
- Export citation
On Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 249-254
-
- Article
-
- You have access
- Export citation
Subgroups of Conjugate Classes in Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 773-783
-
- Article
-
- You have access
- Export citation
On Balanced Incomplete Block Designs with Large Number of Elements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 61-65
-
- Article
-
- You have access
- Export citation
On the ARF Invariant of an Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 519-524
-
- Article
-
- You have access
- Export citation
The Collineation Group of the Veblen-Wedderburn Plane of Order Nine
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 967-973
-
- Article
-
- You have access
- Export citation
Growth and Decay Estimates near Non-Elementary Stationary Points
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1156-1167
-
- Article
-
- You have access
- Export citation
On Direct Products of Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-544
-
- Article
-
- You have access
- Export citation
Point-Transitive Actions by the Unit Interval
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 255-259
-
- Article
-
- You have access
- Export citation
On a Theorem of Heilbronn Concerning the Fractional Part of θn2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 784-788
-
- Article
-
- You have access
- Export citation
Extensions of a Brandt Semigroup by Another
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 974-983
-
- Article
-
- You have access
- Export citation
Ideal Extensions of Topological Semigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1168-1175
-
- Article
-
- You have access
- Export citation
On the Addition of Relations in an Abelian Category
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 66-74
-
- Article
-
- You have access
- Export citation
More on Extending Continuous Pseudometrics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 984-993
-
- Article
-
- You have access
- Export citation
Singular Integrals are Perron Integrals of a Certain Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 260-264
-
- Article
-
- You have access
- Export citation
A Local Ratio Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 545-552
-
- Article
-
- You have access
- Export citation
On Quasi-Essential Subgroups of Primary Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1176-1184
-
- Article
-
- You have access
- Export citation
On the Rank Numbers of an Arc
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 789-802
-
- Article
-
- You have access
- Export citation
Initial Segments of Many-One Degrees
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 75-85
-
- Article
-
- You have access
- Export citation

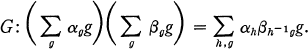
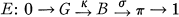
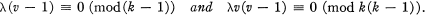
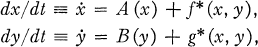
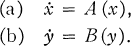




 .
. of relations in an abelian category
of relations in an abelian category  was studied. A relation from
was studied. A relation from 
 , where
, where  is the image of Γ in the canonical involution on
is the image of Γ in the canonical involution on 

 if and only if the square
if and only if the square
 . We denote the integral ∫
. We denote the integral ∫