Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T17:46:27.472Z Has data issue: false hasContentIssue false
  • English
  • Français

On Balanced Incomplete Block Designs with Large Number of Elements

Published online by Cambridge University Press:  20 November 2018

Haim Hanani
Haim Hanani*
Affiliation:
Technion–Israel Institute of Technology, Technion City, Haifa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A balanced incomplete block design (BIBD) B[k, λ; v] is an arrangement of v distinct elements into blocks each containing exactly k distinct elements such that each pair of elements occurs together in exactly λ blocks.

The following is a well-known theorem [5, p. 248].

THEOREM 1. A necessary condition for the existence of a BIBD B[k, λ,v] is that

(1)

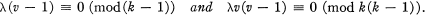
It is also well known [5] that condition (1) is not sufficient for the existence of B[k, λ; v].

There is an old conjecture that for any given k and λ condition (1) may be sufficient for the existence of a BIBD B[k, λ; v] if v is sufficiently large. It is attempted here to prove this conjecture in some specific cases.

There is an old conjecture that for any given k and X condition (1) may be sufficient for the existence of a BIBD B[k, λ; v] if v is sufficiently large. It is attempted here to prove this conjecture in some specific cases.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 1 , 01 February 1970 , pp. 61 - 65
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Bose, R. C. and Shrikhande, S., On the construction of sets of mutually orthogonal Latin squares and the falsity of a conjecture of Euler, Trans. Amer. Math. Soc. 95 (1960), 191–209.Google Scholar
2. Bose, R. C., Parker, E. T., and Shrikhande, S., Further results on the construction of mutually orthogonal Latin squares and the falsity of Euler's conjecture, Can. J. Math. 12 (1960), 189–203.Google Scholar
3. Carmichael, R. D., Introduction to the theory of groups of finite order (Dover, New York, 1956).Google Scholar
4. Chowla, S., Erdös, P., and Straus, E. G., On the maximal number of pairwise orthogonal Latin squares of a given order, Can. J. Math. 12 (1960), 204–208.Google Scholar
5. Hall, M. Jr., Combinatorial theory (Blaisdell, Waltham, Massachusetts, 1967).Google Scholar
6. Hanani, H., The existence and construction of balanced incomplete block designs, Ann. Math. Statist. 82 (1961), 361–386.Google Scholar
7. Hanani, H., A balanced incomplete block design, Ann. Math. Statist. 36 (1965), 711.Google Scholar
8. Hanani, H., On the number of orthogonal Latin squares, J. Combinatorial Theory (to appear).Google Scholar
9. Parker, E., Construction of some sets of mutually orthogonal Latin squares, Proc. Amer. Math. Soc. 10 (1959), 946–949.Google Scholar
10. Rogers, K., A note on orthogonal Latin squares, Pacific J. Math. 14 (1964), 1395–1397.Google Scholar
11. Storer, Th., Cyototomy and difference sets (Markham, Chicago, 1967).Google Scholar