Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T05:55:12.482Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of Heilbronn Concerning the Fractional Part of θn2

Published online by Cambridge University Press:  20 November 2018

Ming-Chit Liu
Ming-Chit Liu*
Affiliation:
University of Hong Kong, Pokfulum Road, Hong Kong
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. In 1948 Heilbronn [4] proved the following theorem.

THEOREM H. For every real θ and every positive integer N, there is an integer n satisfying

(1.1)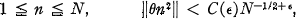

whereis an arbitrarily small number,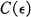depends only on, and ‖t‖ means the distance from t to the nearest integer.

The interest of the result (1.1) is that the inequality is uniform in θ, and is therefore analogous to the classical inequality of Dirichlet for the fractional part of θn. In this paper we shall prove the following theorem.

THEOREM. For every real θ and every positive integer N, there is an integer n satisfying

(1.2)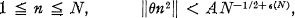

where A is an absolute constant and.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 784 - 788
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Ayoub, R., An introduction to the analytic theory of numbers, Mathematical Surveys, No. 10 (Amer. Math. Soc, Providence, R.I., 1963).Google Scholar
2. Davenport, H., On a theorem of Heilbronn, Quart. J. Math. Oxford Ser. 18 (1967), 339–344.Google Scholar
3. Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, 3rd ed. (Oxford, at the Clarendon Press, 1954).Google Scholar
4. Heilbronn, H., On the distribution of the sequence n20 (mod 1), Quart. J. Math. Oxford Ser. 19 (1948), 249–256.Google Scholar
5. Hua, L. K., Additive theory of prime numbers, Translations of Mathematical Monographs, Vol. 13 (Amer. Math. Soc, Providence, R.I., 1965).Google Scholar
6. Vinogradov, I. M., The method of trigonometric sums in the theory of numbers (Interscience, New York, 1954).Google Scholar