Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T05:23:42.089Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Rank Numbers of an Arc

Published online by Cambridge University Press:  20 November 2018

J. Turgeon
J. Turgeon*
Affiliation:
University of Toronto, Toronto, Ontario Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The kth rank number, rankkB, of a differentiable arc B in real projective n-space is the least upper bound of the number of osculating k-spaces of B which meet an (n – k – l)-flat, k = 0, 1, …, n – 1. The number rank0B is called the order of B; cf. 1.1-1.3. It has been conjectured by Peter Scherk that

(0.1)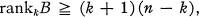

equality holding if and only if B has the order n; cf. [2, p. 396]. In this paper we prove the following results.

THEOREM 1. If B is a differentiable elementary arc, then (0.1) holds for k = 0, 1, …, n – 1.

THEOREM 2. If B is a differentiable elementary arc and order B > n, then rankkB > (k + 1) (n – k) for k = 1, …, n – 2.

By a theorem of Park [3, p. 38], every differentiable arc contains a subarc of order n. This eliminates the assumption that B is elementary from Theorem 1. We do not know whether it can be dropped from Theorem 2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 789 - 802
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Derry, D., The duality theorem for curves of order n in n-space, Can. J. Math. 3 (1951), 159–163.Google Scholar
2. Haupt, O. and H., Kiïnneth, Geometrische Ordnungen, Die Grundlehren der mathematischen Wissenschaften, Band 133 (Springer-Verlag, Berlin-New York, 1967).Google Scholar
3. Park, R., On Barner arcs, Dissertation, University of Toronto, Toronto, Ontario, 1968.Google Scholar
4. Scherk, P., Ùber differenzierbare Kurven und Bögen. I. Zum Begriff der Charakteristik; II. Elementarbogen und Kurventer Ordnung im R n , Casopis Pëst. Mat. Fys. 66 (1937), 165–191.Google Scholar