An $n\times n$ matrix is said to be totally nonnegative if every minor of $A$ is nonnegative. In this paper we completely characterize all possible Jordan canonical forms of irreducible totally nonnegative matrices. Our approach is mostly combinatorial and is based on the study of weighted planar diagrams associated with totally nonnegative matrices.

Contractivity and hypercontractivity properties of semigroups are now well understood when the generator, $A$, is a Dirichlet form operator. It has been shown that in some holomorphic function spaces the semigroup operators, ${{e}^{-tA}}$, can be bounded below from ${{L}^{p}}$ to ${{L}^{q}}$ when $p,\,q$ and $t$ are suitably related. We will show that such lower boundedness occurs also in spaces of subharmonic functions.

We prove a symmetric imprimitivity theorem for commuting proper actions of locally compact groups $H$ and $K$ on a ${{C}^{*}}$-algebra.

We investigate exceptional sets in the Waring–Goldbach problem. For example, in the cubic case, we show that all but $O\left( {{N}^{79/84+\in }} \right)$ integers subject to the necessary local conditions can be represented as the sum of five cubes of primes. Furthermore, we develop a new device that leads easily to similar estimates for exceptional sets for sums of fourth and higher powers of primes.

We describe the structure of the space of second order elliptic differential operators on a homogenous bundle over a compact Lie group. Subject to a technical condition, these operators are homotopic to the Laplacian. The technical condition is further investigated, with examples given where it holds and others where it does not. Since many spectral invariants are also homotopy invariants, these results provide information about the invariants of these operators.

In this paper we make explicit all $L$-functions in the Langlands–Shahidi method which appear as normalizing factors of global intertwining operators in the constant term of the Eisenstein series. We prove, in many cases, the conjecture of Shahidi regarding the holomorphy of the local $L$-functions. We also prove that the normalized local intertwining operators are holomorphic and non-vaninishing for $\operatorname{Re}\left( s \right)\,\ge \,1/2$ in many cases. These local results are essential in global applications such as Langlands functoriality, residual spectrum and determining poles of automorphic $L$-functions.

We consider some deformations of ${{G}_{2}}$-structures on 7-manifolds. We discover a canonical way to deform a ${{G}_{2}}$-structure by a vector field in which the associated metric gets “twisted” in some way by the vector cross product. We present a system of partial differential equations for an unknown vector field $w$ whose solution would yield a manifold with holonomy ${{G}_{2}}$. Similarly we consider analogous constructions for Spin(7)-structures on 8-manifolds. Some of the results carry over directly, while others do not because of the increased complexity of the Spin(7) case.

Let $K$ be a function on a unimodular locally compact group $G$, and denote by ${{K}_{n}}\,=\,K\,*\,K\,*\cdots *\,K$ the $n$-th convolution power of $K$. Assuming that $K$ satisfies certain operator estimates in ${{L}^{2}}\left( G \right)$, we give estimates of the norms ${{\left\| {{K}_{n}} \right\|}_{2}}$ and ${{\left\| {{K}_{n}} \right\|}_{\infty }}$ for large $n$. In contrast to previous methods for estimating ${{\left\| {{K}_{n}} \right\|}_{\infty }}$, we do not need to assume that the function $K$ is a probability density or nonnegative. Our results also adapt for continuous time semigroups on $G$. Various applications are given, for example, to estimates of the behaviour of heat kernels on Lie groups.

We study closed extensions $\underset{\scriptscriptstyle-}{A}$ of an elliptic differential operator $A$ on a manifold with conical singularities, acting as an unbounded operator on a weighted ${{L}_{p}}$-space. Under suitable conditions we show that the resolvent ${{\left( \lambda -\underset{\scriptscriptstyle-}{A} \right)}^{-1}}$ exists in a sector of the complex plane and decays like $1/\left| \lambda \right|$ as $\left| \lambda \right|\to \infty $. Moreover, we determine the structure of the resolvent with enough precision to guarantee existence and boundedness of imaginary powers of $\underset{\scriptscriptstyle-}{A}$.

As an application we treat the Laplace–Beltrami operator for a metric with straight conical degeneracy and describe domains yielding maximal regularity for the Cauchy problem $\dot{u}\,-\,\Delta u\,=\,f,$$u\left( 0 \right)\,=\,0$.

Let $E/\mathbb{Q}$ be an elliptic curve defined by the equation ${{y}^{2}}\,=\,{{x}^{3}}\,+\,ax\,+\,b.$ For a prime $p$, $p\nmid \Delta \,=\,-16\left( 4{{a}^{3}}+27{{b}^{2}} \right)\,\ne \,0,$ define

$${{N}_{p}}=p+1-{{a}_{p}}=\,\left| E\left( {{\mathbb{F}}_{p}} \right) \right|.$$

As a precursor to their celebrated conjecture, Birch and Swinnerton-Dyer originally conjectured that for some constant $c$,

$$\prod\limits_{p\le x,p\nmid \Delta }{\frac{{{N}_{p}}}{p}\,\sim \,c{{\left( \log x \right)}^{r}},\,\,\,x\to \infty .}$$

Let ${{\alpha }_{p}}$ and ${{\beta }_{p}}$ be the eigenvalues of the Frobenius at $p$. Define

$${{\tilde{c}}_{n}}=\left\{ \begin{align} & \frac{\alpha _{p}^{k}+\beta _{P}^{k}}{k}\,\,\,\,n={{p}^{k}},\,p\,\text{is}\,\text{a}\,\text{prime,}\,k\,\text{is}\,\text{a}\,\text{natural}\,\text{number},\,p\nmid \Delta . \\ & 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{otherwise} \\ \end{align} \right.\,$$

and $\tilde{C}\left( x \right)\,=\,\sum\nolimits_{n\le x}{{{{\tilde{c}}}_{n}}.}$ In this paper, we establish the equivalence between the conjecture and the condition $\tilde{C}\left( x \right)\,=\,\mathbf{o}\left( x \right).$ The asymptotic condition is indeed much deeper than what we know so far or what we can know under the analogue of the Riemann hypothesis. In addition, we provide an oscillation theorem and an $\Omega $ theorem which relate to the constant $c$ in the conjecture.

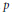The main result of the paper is a reciprocity law which proves that compatible systems of semisimple, abelian mod $p$ representations (of arbitrary dimension) of absolute Galois groups of number fields, arise from Hecke characters. In the last section analogs for Galois groups of function fields of these results are explored, and a question is raised whose answer seems to require developments in transcendence theory in characteristic $p$.

For a given elliptic curve $\mathbf{E}$, we obtain an upper bound on the discrepancy of sets of multiples ${{z}_{s}}G$ where ${{z}_{s}}$ runs through a sequence $Z\,=\,\left( {{z}_{1}},\ldots ,{{z}_{T}} \right)$ such that $k{{z}_{1}},\ldots ,k{{z}_{T}}$ is a permutation of ${{z}_{1}},\ldots ,{{z}_{T}}$, both sequences taken modulo $t$, for sufficiently many distinct values of $k$ modulo $t$.

We apply this result to studying an analogue of the power generator over an elliptic curve. These results are elliptic curve analogues of those obtained for multiplicative groups of finite fields and residue rings.

Let ${{E}_{/\mathbb{Q}}}$ be an elliptic curve with good ordinary reduction at a prime $p\,>\,2$. It has a welldefined Iwasawa $\mu $-invariant $\mu {{\left( E \right)}_{p}}$ which encodes part of the information about the growth of the Selmer group $\text{Se}{{\text{l}}_{{{p}^{\infty }}}}\left( {{E}_{/{{K}_{n}}}} \right)$ as ${{K}_{n}}$ ranges over the subfields of the cyclotomic ${{\mathbb{Z}}_{p}}$-extension ${{K}_{\infty }}/\mathbb{Q}$. Ralph Greenberg has conjectured that any such $E$ is isogenous to a curve ${E}'$ with $\mu {{\left( {{E}'} \right)}_{p}}\,=\,0$. In this paper we prove Greenberg's conjecture for infinitely many curves $E$ with a rational $p$-torsion point, $p$ = 3 or 5, no two of our examples having isomorphic $p$-torsion. The core of our strategy is a partial explicit evaluation of the global duality pairing for finite flat group schemes over rings of integers.

Differential operators ${{D}_{x,}}\,{{D}_{y}}$, and ${{D}_{z}}$ are formed using the action of the 3-dimensional discrete Heisenberg group $G$ on a set $S$, and the operators will act on functions on $S$. The Laplacian operator $L\,=\,D_{x}^{2}+D_{y}^{2}+D_{z}^{2}$ is a difference operator with variable differences which can be associated to a unitary representation of $G$ on the Hilbert space ${{L}^{2}}\left( S \right)$. Using techniques from harmonic analysis and representation theory, we show that the Laplacian operator is locally solvable.

Let $\ell $ be a length function on a group $G$, and let ${{M}_{\ell }}$ denote the operator of pointwise multiplication by $\ell $ on ${{\ell }^{2}}\left( G \right)$. Following Connes, ${{M}_{\ell }}$ can be used as a “Dirac” operator for $C_{r}^{*}\left( G \right)$. It defines a Lipschitz seminorm on $C_{r}^{*}\left( G \right)$, which defines a metric on the state space of $C_{r}^{*}\left( G \right)$. We show that if $G$ is a hyperbolic group and if $\ell $ is a word-length function on $G$, then the topology from this metric coincides with the weak-$*$ topology (our definition of a “compact quantum metric space”). We show that a convenient framework is that of filtered ${{C}^{*}}$-algebras which satisfy a suitable “Haagerup-type” condition. We also use this framework to prove an analogous fact for certain reduced free products of ${{C}^{*}}$-algebras.

We study certain symplectic quotients of $n$-fold products of complex projective $m$-space by the unitary group acting diagonally. After studying nonemptiness and smoothness of these quotients we construct the action-angle variables, defined on an open dense subset, of an integrable Hamiltonian system. The semiclassical quantization of this system reporduces formulas from the representation theory of the unitary group.

The original Gelfond–Schnirelman method, proposed in 1936, uses polynomials with integer coefficients and small norms on [0, 1] to give a Chebyshev-type lower bound in prime number theory. We study a generalization of this method for polynomials in many variables. Our main result is a lower bound for the integral of Chebyshev's $\psi $-function, expressed in terms of the weighted capacity. This extends previous work of Nair and Chudnovsky, and connects the subject to the potential theory with external fields generated by polynomial-type weights. We also solve the corresponding potential theoretic problem, by finding the extremal measure and its support.

In this paper, we construct a duality for $p$-adic orthogonal groups.

Let $A$ be an amenable separable ${{C}^{*}}$-algebra and $B$ be a non-unital but $\sigma $-unital simple ${{C}^{*}}$- algebra with continuous scale. We show that two essential extensions ${{\tau }_{1}}$ and ${{\tau }_{2}}$ of $A$ by $B$ are approximately unitarily equivalent if and only if

$$\left[ {{\tau }_{1}} \right]\,=\,\left[ {{\tau }_{2}} \right]\,\text{in}\,KL\left( A,\,M\left( B \right)/B \right).$$

If $A$ is assumed to satisfy the Universal Coefficient Theorem, there is a bijection from approximate unitary equivalence classes of the above mentioned extensions to $KL\left( A,\,M\left( B \right)/B \right)$. Using $KL\left( A,\,M\left( B \right)/B \right)$, we compute exactly when an essential extension is quasidiagonal. We show that quasidiagonal extensions may not be approximately trivial. We also study the approximately trivial extensions.

Estimating the degree of approximation in the uniform norm, of a convex function on a finite interval, by convex algebraic polynomials, has received wide attention over the last twenty years. However, while much progress has been made especially in recent years by, among others, the authors of this article, separately and jointly, there have been left some interesting open questions. In this paper we give final answers to all those open problems. We are able to say, for each $r$-th differentiable convex function, whether or not its degree of convex polynomial approximation in the uniform norm may be estimated by a Jackson-type estimate involving the weighted Ditzian–Totik $k$th modulus of smoothness, and how the constants in this estimate behave. It turns out that for some pairs $(k,\,r)$ we have such estimate with constants depending only on these parameters. For other pairs the estimate is valid, but only with constants that depend on the function being approximated, while there are pairs for which the Jackson-type estimate is, in general, invalid.