Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-18T13:50:15.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformations of G2 and Spin(7) Structures

Published online by Cambridge University Press:  20 November 2018

Spiro Karigiannis
Spiro Karigiannis*
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

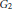We consider some deformations of ${{G}_{2}}$-structures on 7-manifolds. We discover a canonical way to deform a 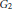${{G}_{2}}$-structure by a vector field in which the associated metric gets “twisted” in some way by the vector cross product. We present a system of partial differential equations for an unknown vector field $w$ whose solution would yield a manifold with holonomy 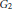${{G}_{2}}$. Similarly we consider analogous constructions for Spin(7)-structures on 8-manifolds. Some of the results carry over directly, while others do not because of the increased complexity of the Spin(7) case.

Keywords

53C2653C29G2 Spin(7)holonomymetricscross product
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 5 , 01 October 2005 , pp. 1012 - 1055
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Bonan, E., Sur des Variétés riemanniennes à groupe d’holonomie G2 ou Spin(7). C. R. Acad. Sci. Paris 262(1966), 127–129.Google Scholar
[2] Brown, R. B. and Gray, A., Vector Cross Products. Comment.Math. Helv. 42(1967), 222–236.Google Scholar
[3] Bryant, R. L., Metrics with Exceptional Holonomy. Ann. of Math. 126(1987), 525–576.Google Scholar
[4] Bryant, R. L. and Salamon, S. M., On the Construction of Some Complete Metrics with Exceptional Holonomy. Duke Math. J. 58(1989), 829–850.Google Scholar
[5] Cabrera, F. M., On Riemannian Manifolds with G2-Structure. Boll. Un.Mat. Ital. A (7) 10(1996), 99–112.Google Scholar
[6] Cabrera, F. M., Monar, M. D. and Swann, A. F., Classification of G2-Structures. J. London Math. Soc (2) 53(1996), 407–416.Google Scholar
[7] Fernández, M., A Classification of Riemannian Manifolds with Structure Group Spin(7). Ann.Mat. Pura Appl. (IV) 143(1986), 101–122.Google Scholar
[8] Fernández, M., An Example of a Compact Calibrated Manifold Associated with the Exceptional Lie Group G2. J. Differential Geom. 26(1987), 367–370.Google Scholar
[9] Fernández, M. and Gray, A., Riemannian Manifolds with Structure Group G2 . Ann. Mat. Pura Appl (4) 32(1982), 19–45.Google Scholar
[10] Fernández, M. and Ugarte, L., Dolbeault Cohomology for G2-Manifolds. Geom. Dedicata 70(1998), 57–86.Google Scholar
[11] Fernández, M., A Differential Complex for Locally Conformal Calibrated G2-Manifolds. Illinois J. Math. 44(2000), 363–391.Google Scholar
[12] Gray, A., Vector Cross Products on Manifolds. Trans. Amer.Math. Soc. 141(1969), 463–504; Errata to “Vector Cross Products onManifolds”. 148(1970), 625.Google Scholar
[13] Gray, A., Weak Holonomy Groups. Math. Z. 123(1971), 290–300.Google Scholar
[14] Gray, A. and Hervella, L. M., The Sixteen Classes of Almost Hermitian Manifolds and Their Linear Invariants. Ann.Mat. Pura Appl. (4) 123(1980), 35–58.Google Scholar
[15] Gukov, S., Yau, S. T. and Zaslow, E., Duality and Fibrations on G2 Manifolds. Turkish J. Math. 27(2003), 61–97.Google Scholar
[16] Harvey, R., Spinors and Calibrations. Academic Press, San Diego, 1990.Google Scholar
[17] Hitchin, N., The Geometry of Three-Forms in Six and Seven Dimensions. J. Differential Geom. 55(2000), 547–576.Google Scholar
[18] Hitchin, N., Stable Forms and Special Metrics. Global Differential Geometry: The Mathematical Legacy of Alfred Gray, Contemp.Math. 288(2001).Google Scholar
[19] Joyce, D. D., Compact Riemannian 7-Manifolds with Holonomy G2. I. J. Differential Geom. 43(1996), 291–328.Google Scholar
[20] Joyce, D. D., Compact Riemannian 7-Manifolds with Holonomy G2. II. J. Differential Geom. 43(1996), 329–375.Google Scholar
[21] Joyce, D. D., Compact 8-Manifolds with Holonomy Spin(7). Invent.Math. 123(1996), 507–552.Google Scholar
[22] Joyce, D. D., Compact Manifolds with Special Holonomy. Oxford University Press, Oxford, 2000.Google Scholar
[23] Karigiannis, S., Deformations of G2 and Spin(7)-structures on Manifolds. long version, http://arxiv.org/archive/math.DG/0301218.Google Scholar
[24] Karigiannis, S., On a system of PDE's related to G2 holonomy. in preparation.Google Scholar
[25] Salamon, S. M., Riemannian Geometry and Holonomy Groups. Longman Group UK Limited, Harlow, 1989.Google Scholar
[26] Yau, S. T., On the Ricci Curvature of a Compact Kähler Manifold and the Complex Monge–Ampère Equation I. Comm. Pure Appl. Math. 31(1978), 339–411.Google Scholar