Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T06:19:22.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Convex Polynomial Approximation in the Uniform Norm: Conclusion

Published online by Cambridge University Press:  20 November 2018

K. A. Kopotun ,
D. Leviatan  and
I. A. Shevchuk
K. A. Kopotun
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, MB, R3T 2N2, e-mail: [email protected]
D. Leviatan
Affiliation:
School of Mathematical Sciences, Raymond and Beverley Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv 69978, Israel, e-mail: [email protected]
I. A. Shevchuk
Affiliation:
Faculty of Mechanics and Mathematics, National Taras Shevchenko University of Kyiv, Kyiv 01033, Ukraine, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Estimating the degree of approximation in the uniform norm, of a convex function on a finite interval, by convex algebraic polynomials, has received wide attention over the last twenty years. However, while much progress has been made especially in recent years by, among others, the authors of this article, separately and jointly, there have been left some interesting open questions. In this paper we give final answers to all those open problems. We are able to say, for each $r$-th differentiable convex function, whether or not its degree of convex polynomial approximation in the uniform norm may be estimated by a Jackson-type estimate involving the weighted Ditzian–Totik $k$th modulus of smoothness, and how the constants in this estimate behave. It turns out that for some pairs 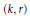$(k,\,r)$ we have such estimate with constants depending only on these parameters. For other pairs the estimate is valid, but only with constants that depend on the function being approximated, while there are pairs for which the Jackson-type estimate is, in general, invalid.

Keywords

41A1041A2541A29
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1224 - 1248
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] DeVore, R. A. and Lorentz, G. G., Constructive approximation, Grundlehren derMathematischenWissenschaften [Fundamental Principles of Mathematical Sciences] 303. Springer-Verlag, Berlin, 1993.Google Scholar
[2] DeVore, R. A., Leviatan, D., and Shevchuk, I. A., Approximation of monotone functions: a counter ex- ample. In: Curves and surfaces with applications in CAGD (Chamonix–Mont-Blanc, 1996), 1997, pp. 95–102.Google Scholar
[3] Ditzian, Z. and Totik, V., Moduli of smoothness, Springer Series in Computational Mathematics 9. Springer-Verlag, New York, 1987.Google Scholar
[4] Dzyadyk, V. K., Constructive characterization of functions satisfying the condition Lip ∞(0 < ∞ < 1) on a finite segment of the real axis. Izv. Akad. Nauk SSSR. Ser. Mat. 20(1956), 623–642 (Russian).Google Scholar
[5] Hu, Y., Leviatan, D., and Yu, X.M., Convex polynomial and spline approximation in C [−1, 1]. Constr. Approx. 10(1994), 31–64.Google Scholar
[6] Kopotun, K. A., Uniform estimates for coconvex approximation of functions by polynomials. Mat. Zametki 51(1992), 35–46 (Russian; translation in Math. Notes 51 (1992), 245–254).Google Scholar
[7] Kopotun, K. A., Pointwise and uniform estimates for convex approximation of functions by algebraic polyno- mials. Constr. Approx. 10(1994), 153–178.Google Scholar
[8] Kopotun, K. A., Uniform estimates of monotone and convex approximation of smooth functions. J. Approx. Theory 80(1995), 76–107.Google Scholar
[9] Kopotun, K. A., Simultaneous approximation by algebraic polynomials. Constr. Approx. 12(1996), 67–94.Google Scholar
[10] Kopotun, K. A. and Listopad, V. V., Remarks on monotone and convex approximation by algebraic poly- nomials. Ukraïn.Mat. Zh. 46(1994), 1266–1270 (English, with English and Ukrainian summaries).Google Scholar
[11] Leviatan, D., Pointwise estimates for convex polynomial approximation. Proc. Amer. Math. Soc. 98(1986), 471–474.Google Scholar
[12] Leviatan, D. and Shevchuk, I. A., Some positive results and counterexamples in comonotone approxima- tion. II. J. Approx. Theory 100(1999), 113–143.Google Scholar
[13] Leviatan, D. and Shevchuk, I. A., Coconvex approximation. J. Approx. Theory 118(2002), 20–65.Google Scholar
[14] Leviatan, D. and Shevchuk, I. A., Coconvex polynomial approximation. J. Approx. Theory 121(2003), 100–118.Google Scholar
[15] Nissim, R. and Yushchenko, L. P., Negative result for nearly q-convex approximation. East J. Approx. 9(2003), 209–213.Google Scholar
[16] Shevchuk, I. A., Approximation by Polynomials and Traces of the Functions Continuous on an Interval. Naukova Dumka, Kyiv, 1992.Google Scholar
[17] Švedov, A. S., Orders of coapproximation of functions by algebraic polynomials.Mat. Zametki 29(1981), 117–130, 156 (Russian).Google Scholar
[18] X.Wu and Zhou, S. P., On a counterexample in monotone approximation. J. Approx. Theory 69(1992), 205–211.Google Scholar