Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-18T14:15:28.590Z Has data issue: false hasContentIssue false
  • English
  • Français

The Gelfond–Schnirelman Method in Prime Number Theory

Published online by Cambridge University Press:  20 November 2018

Igor E. Pritsker
Igor E. Pritsker*
Affiliation:
Department of Mathematics, 401 Mathematical Sciences, Oklahoma State University, Stillwater, OK 74078-1058, U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The original Gelfond–Schnirelman method, proposed in 1936, uses polynomials with integer coefficients and small norms on [0, 1] to give a Chebyshev-type lower bound in prime number theory. We study a generalization of this method for polynomials in many variables. Our main result is a lower bound for the integral of Chebyshev's 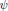$\psi $-function, expressed in terms of the weighted capacity. This extends previous work of Nair and Chudnovsky, and connects the subject to the potential theory with external fields generated by polynomial-type weights. We also solve the corresponding potential theoretic problem, by finding the extremal measure and its support.

Keywords

Primary: 11N0531A15secondary: 11C08distribution of prime numberspolynomialsinteger coefficientsweighted transfinite diameterweighted capacitypotentials
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 5 , 01 October 2005 , pp. 1080 - 1101
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Amoroso, F., f -transfinite diameter and number theoretic applications. Ann. Inst. Fourier (Grenoble) 43(1993), 1179–1198.Google Scholar
[2] Andrievskii, V. V. and Blatt, H.-P., Discrepancy of Signed Measures and Polynomial Approximation. Springer-Verlag, New York, 2002.Google Scholar
[3] Bloom, T. and Calvi, J. P., On the multivariate transfinite diameter. Ann. Polon. Math. 72(1999), 285–305.Google Scholar
[4] Bloom, T. and Calvi, J. P., On multivariate minimal polynomials. Math. Proc. Cambridge Philos. Soc. 129(2000), 417–431.Google Scholar
[5] Borwein, P., Computational Excursions in Analysis and Number Theory. CMS Books in Mathematics 10, Springer-Verlag, New York, 2002.Google Scholar
[6] Chebyshev, P. L., CollectedWorks. Vol. 1, Akad. Nauk SSSR, Moscow, 1944. (Russian)Google Scholar
[7] Chudnovsky, G. V., Number theoretic applications of polynomials with rational coefficients defined by extremality conditions. In: Arithmetic and Geometry, Vol. I, (Artin, M. and Tate, J., eds.), Birkhäuser, Boston, 1983, pp. 61–105.Google Scholar
[8] Davenport, H.,Multiplicative Number Theory. Second edition. Springer-Verlag, New York, 1980.Google Scholar
[9] Deift, P., Kreicherbauer, T., and McLaughlin, K. T.-R., New results on the equilibrium measure for logarithmic potentials in the presence of an external field. J. Approx. Theory 95(1998), 388–475.Google Scholar
[10] Diamond, H. G., Elementary methods in the study of the distribution of prime numbers. Bull. Amer. Math. Soc. 7(1982), 553–589.Google Scholar
[11] Erdʺos, P., On a new method in elementary number theory which leads to an elementary proof of the prime number theorem, Proc. Nat. Acad. Sci. U.S.A. 35(1949), 374–384.Google Scholar
[12] Fekete, M., Über die Verteilung derWurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten. Math. Zeit. 17(1923), 228–249.Google Scholar
[13] Frostman, O., La méthode de variation de Gauss et les fonctions sousharmoniques. Acta Sci. Math. 8(1936/37), 149–159.Google Scholar
[14] Gauss, C. F., Allgemeine Lehrsätze in Beziehung auf die in verkehrten Verhältnissen des Quadrats der Entfernung wirkenden Anzienhungs- und Abstossungs- Kräfte. In: Werke, Band 5, Göttingen, 1840, pp. 197–242.Google Scholar
[15] Gorshkov, D. S., On the distance from zero on the interval [0, 1] of polynomials with integral coefficients. In: Proc. of the Third All UnionMathematical Congress, Vol. 4, Akad. Nauk SSSR, Moscow, 1959, pp. 5–7. (Russian)Google Scholar
[16] Götz, M. and Saff, E. B., Potential and discrepancy estimates for weighted extremal points. Constr. Approx. 16(2000), 541–557.Google Scholar
[17] Ingham, A. E., The Distribution of Prime Numbers. Cambridge University Press, Cambridge, 1932.Google Scholar
[18] Klimek, M., Pluripotential Theory. LondonMathematical Monographs New Series 6, Oxford University Press, New York, 1991.Google Scholar
[19] Montgomery, H. L., Ten Lectures on the Interface Between Analytic Number Theory and Harmonic Analysis. CBMS Regional Conference Series in Mathematics 84, American Mathematical Society, Providence, RI, 1994.Google Scholar
[20] Muskhelishvili, N. I., Singular Integral Equations. Dover, New York, 1992.Google Scholar
[21] Nair, M., A new method in elementary prime number theory. J. LondonMath. Soc. (2) 25(1982), 385–391.Google Scholar
[22] Pritsker, I. E., Small polynomials with integer coefficients. J. Anal. Math. (to appear); available electronically at http://www.math.okstate.edu/˜igor/intcheb.psGoogle Scholar
[23] Ransford, T., Potential Theory in the Complex Plane. LondonMathematial Society Student Texts 28, Cambridge University Press, Cambridge, 1995.Google Scholar
[24] Riemann, B., Über die Anzahl der Primzahlen unter einer gegebenen Grösse. In: Werke, Teubner, Leipzig, 1892, pp. 145–155.Google Scholar
[25] Saff, E. B. and Totik, V., Logarithmic Potentials with External Fields. Grundlehren der MathematischenWissenschafter 316, Springer-Verlag, Berlin, 1997.Google Scholar
[26] Selberg, A., An elementary proof of the prime-number theorem. Ann. of Math. 50(1949), 305–313.Google Scholar
[27] Stahl, H. and Totik, V., General Orthogonal Polynomials. Encyclopedia of Mathematics and its Applications 43, Cambridge University Press, Cambridge, 1992.Google Scholar
[28] Szegʺo, G., Bemerkungen zu einer Arbeit von Herrn M. Fekete: Über die Verteilung derWurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten, Math. Zeit. 21(1924), 203–208.Google Scholar
[29] Tenenbaum, G. and France, M. M., The Prime Numbers and Their Distribution. Student Mathematical Library 6, American Mathematical Society, Providence, RI, 2000.Google Scholar
[30] Totik, V., Polynomial inverse images and polynomial inequalities. Acta Math. 187(2001), 139–160.Google Scholar
[31] Trigub, R. M., Approximation of functions with Diophantine conditions by polynomials with integral coefficients. In: Metric Questions of the Theory of Functions and Mappings, Naukova Dumka, Kiev, 1971, pp. 267–333. (Russian)Google Scholar
[32] Zaharjuta, V. P., Transfinite diameter, Čebyšev constants, and capacity for compacta in Cn. Mat. Sb. 96(1975), 347–389.Google Scholar