This paper studies how coding theory and group theory can be used to produce information about a finite projective plane π and a collineation group G of π.

A new proof for Hering's bound on |G| is given in 2.5. Using the idea of coding theory developed in [9], a relation between two rows of the incidence matrix of π with respect to a tactical decomposition is obtained in 2.1. This result yields, among other things, some techniques in calculating |G|, and generalizes a result of Roth [16], [see 2.4 and 2.5].

Hering [7] introduced the notion of strong irreducibility of G, that is, G does not leave invariant any point, line, triangle or proper subplane. He showed that if in addition G contains a non-trivial perspectivity, then there is a unique minimal normal subgroup of G. This subgroup is either non-abelian simple or isomorphic to the elementary abelian group Z3 × Z3 of order 9.

In [11] G. G. Kasparov defined the “operator K-functor” KK(A, B) associated with the graded C*-algebras A and B. If the algebras A and B are trivially graded and A is nuclear he proves six term exact sequence theorems. He asks whether this extends to the graded case.

Here we prove such “six-term exact sequence” results in the graded case. Our proof does not use nuclearity of the algebra A. This condition is replaced by a completely positive lifting condition (Theorem 1.1).

Using our result we may extend the results by M. Pimsner and D. Voiculescu on the K groups of crossed products by free groups to KK groups [15]. We give however a different way of computing these groups using the equivariant KK-theory developed by G. G. Kasparov in [12]. This method also allows us to compute the KK groups of crossed products by PSL2(Z).

In the duality for locally compact groups, much use is made of a version of the Hopf algebra technique in the context of von Neumann algebras, culminating in the theory of Kac algebras [6], [14]. It seems natural to ask whether something like a Hopf algebraic structure can be defined on the pre-dual of a Kac algebra. This leads to the question of whether the multiplication on a von Neumann algebra M, viewed as a linear map m from M ⊙ M (the algebraic tensor product) to M, can be pre-transposed to give a co-multiplication on the pre-dual M*, i.e., a linear map m* from M* to the completion of M* ⊙ M* with respect to some cross-norm. A related question is whether the multiplication on a C*-algebra A can be transposed to give a co-multiplication on the dual A*. Of course, this can be regarded as a special case of the preceding question by taking M = A**, where the double dual A** is identified with the enveloping von Neumann algebra of A.

In this article our purpose is to prove a differentiation theorem for multiparameter processes which are strongly superadditive with respect to a strongly continuous semigroup of positive L1 contractions (see Section 1 for definitions).

Recently, the differentiation theorem for superadditive processes with respect to a one-parameter semigroup of positive L1-contractions has been proved by D. Feyel [9]. Another proof is given by M. A. Akçoğlu [1]. R. Emilion and B. Hachem [7] also proved the same theorem, but with an extra assumption on the process (see also [1]). The proof of this theorem for superadditive processes with respect to a Markovian semigroup of operators on L1 is given by M. A. Akçoğlu and U. Krengel [4]. Thus [1] and [9] extend the result of [4] to the sub-Markovian setting. Here we will obtain the multiparameter sub-Markovian version of this theorem, namely Theorem 3.17 below

A group G is said to have the subnormal join property (s.j.p.) if the join of two (and hence of finitely many) subnormal subgroups of G is always subnormal in G. Following Robinson [6], we shall denote the class of groups having this property by . A particular subclass of is , consisting of those groups G in which the join of two subnormals is again subnormal in G and has defect bounded in terms of the defects of the constituent subgroups (for a more precise definition see Section 7 of [6]).

In [16], Wielandt showed that groups which satisfy the maximal condition for subnormal subgroups have the s.j.p. Many further results on groups with the s.j.p. were proved in [6] and [7]. In Sections 2 and 3 of this paper, it will be shown that several of these results can be exhibited as corollaries of a few rather more general theorems on the classes , .

In recent years there has been considerable attention paid to the behavior of solutions of elliptic boundary value problems in domains with piecewise smooth boundary. In two dimensions the study concerns the behavior of a solution near a corner, and in three (or more) dimensions two cases have been given considerable attention: a conical vertex on the boundary, or an edge.

The solution of such a problem may be singular at the nonsmooth boundary points. The standard example in two dimensions is a solution in polar coordinates of the Dirichlet problem near a corner of interior angle πα;u = r1/α sin θ/α is a function which is harmonic in the sector 0 < θ < πα, has zero boundary values near the corner, and yet at the origin has unbounded derivatives of order > 1/α unless 1/α is an integer.

Let M be a σ-finite von Neumann algebra and {σt}t∊T be a σ-weakly continuous representation of the unit circle, T, as *-automorphisms of M. Let H∞(σ) be the set of all x ∊ M such that

The structure of H∞(σ) was studied by several authors (see [2-13]).

The main object of this paper is to study the σ-weakly closed subalgebras of M that contain H∞(σ). In [12] this was done for the special case where H∞(σ) is a nonselfadjoint crossed product.

Let Mn, for n ∊ Z, be the set of all x ∊ M such that

Let R be a commutative ring, G a finite abelian group of order n and exponent m, and assume n is a unit in R. In [10], F. W. Long defined a generalized Brauer group, BD(R, G), of algebras with a G-action and G-grading, whose elements are equivalence classes of G-Azumaya algebras. In this paper we investigate the automorphisms of a G-Azumaya algebra A and prove that if Picm(R) is trivial, then these automorphisms are all, in some sense, inner.

In fact, each of these “inner” automorphisms can be written as the composition of an inner automorphism in the usual sense and a “linear“ automorphism, i.e., an automorphism of the type

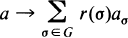
with r(σ) a unit in R. We then use these results to show that the group of gradings of the centre of a G-Azumaya algebra A is a direct summand of G, and thus if G is cyclic of order pr, A is the (smash) product of a commutative and a central G-Azumaya algebra.

The classical four-vertex theorem states that a simple closed convex C2 curve in the Euclidean plane has at least four vertices (points of extreme curvature). This theorem has many generalizations with regard to both the curve and the topological space and for a history of the subject, we refer to [4] and [1]. The particular generalization of concern, credited to H. Mohrmann, is the following n-vertex theorem.

Let a simple closed C3 curve on a closed convex surface be intersected by a suitable plane in n points. Then the curve has at least n inflections (vertices).

The closed convex surface in the preceding is defined as having at most two points in common with any straight line. Presently, we extend this result to curves on more general convex surfaces in a real projective three-space P3.

One aspect of the study of 3-manifolds is to determine what finite group actions a given manifold has. Some important questions that one can ask about these actions on a given manifold are: What periods could they have? and, what sets of points may be fixed by the action? In the case of periodic transformations of homology spheres, Smith [18] classified the types of fixed point sets which could occur. For homology 3-spheres the fixed point set will be ∅, S0, S1, or S2. Fox [4] looked at periodic transformations of the three sphere which leave a knot invariant and, using Smith's classification of fixed point sets, determined that there were eight types of transformations according to how the fixed point set met the knot. For convenience we shall say a knot is (a, b)-periodic if there is a periodic transformation of S3 leaving the knot invariant with fixed point set homeomorphic to a and with the fixed point set meeting the knot in a set homeomorphic to b.

One of the most basic theorems in harmonic analysis on locally compact commutative groups is Bochner's theorem (see [16, p. 19]). This theorem characterizes the positive definite functions. In 1971, R. Lindhal and P. H. Maserick proved a version of Bochner's theorem for discrete commutative semigroups with identity and with an involution * (see [13]). Later, in 1980, C. Berg and P. H. Maserick in [6] generalized this theorem for exponentially bounded positive definite functions on discrete commutative semigroups with identity and with an involution *. In this work we develop these results, and also the Hausdorff moment theorem, for an extensive class of topological semigroups, the so-called “foundation topological semigroups”. We shall give examples to show that these theorems do not extend in the obvious way to general locally compact topological semigroups.

The ergodic theorem for multidimensional strongly subadditive processes relative to a semigroup induced by a measure preserving point transformation on X was proved by R. T. Smythe [18]. His results have been generalized by M. A. Akçoğlu and U. Krengel [4] to the continuous parameter case. The definition of superadditivity they used is stronger than Smythe's but weaker than strong superadditivity. R. Emilion and B. Hachem [10] extended this result to strongly superadditive processes relative to a semigroup generated by a pair of commuting Markovian operators which are also L∞-contractions. The basic tool in the proof is a technique which may be referred to as “reduction of dimension“ and they used a version of it due to A. Brunei [6].

The purpose of this paper is to show that if F = {F(uv)}u>0 is a bounded strongly superadditive process with respect to a two-dimensional strongly continuous Markovian semigroup of operators on L1, then u-2F(uu) converges a.e. as u → ∞.

In [57] (2.12), D. S. Scott showed that the continuous lattices, invented by him in his study of a mathematical theory of computation [56], are precisely (when they are made into topological spaces via the Scott topology) the injective T0-spaces, i.e., the injective objects in the category T0 of T0-spaces and continuous maps with regard to the class of all embeddings. Moreover, the sort of morphisms between continuous lattices Scott considered are precisely the continuous maps with regard to the respective Scott topologies. These are fairly non-Hausdorff topologies. (Indeed, the Scott topology induces the partial order of the lattice L via x ≦ y if and only if x ∊ cl{j}, the “specialization order” of the topology; hence L is Hausdorff in the Scott topology if and only if L has at most one element.) In topological algebra, compact Lawson semilattices (= compact Hausdorff topological ∧-semilattices such that the ∧-preserving continuous maps into the unit interval, with its ordinary topology and the min-semilattice structure, separate the points) with a unit element 1 have attracted considerable interest.

Let G be a locally compact group and ω a normalized multiplier on G. Denote by V(G) (respectively by V(G, ω)) the von Neumann algebra generated by the regular representation (respectively co-regular representation) of G. Kaniuth [6] and Taylor [14] have characterized those G for which the maximal type I finite central projection in V(G) is non-zero (respectively the identity operator in V(G)).

In this paper we determine necessary and sufficient conditions on G and ω such that the maximal type / finite central projection in V(G, ω) is non-zero (respectively the identity operator in V(G, ω)) and construct this projection explicitly as a convolution operator on L2(G). As a consequence we prove the following statements are equivalent,

• (i) V(G, ω) is type I finite,

• (ii) all irreducible multiplier representations of G are finite dimensional,

• (iii) Gω (the central extension of G) is a Moore group, that is all its irreducible (ordinary) representations are finite dimensional.

Let G be a subgroup of the general linear group GL(n, Q) over the rational field Q, and consider its action by right multiplication on the vector space Qn of n-tuples over Q. The present paper investigates the question of how we may constructively determine the orbits and stabilizers of this action for suitable classes of groups. We suppose that G is specified by a finite set {x1, …, xr) of generators, and investigate whether there exist algorithms to solve the two problems:

(Orbit Problem) Given u, v ∊ Qn, does there exist x ∊ G such that ux = v; if so, find such an element x as a word in x1, …, xr and their inverses.

(Stabilizer Problem) Given u, v ∊ Qn, describe all words in x1, …, xr and their inverses which lie in the stabilizer

Throughout this paper when we refer to a semilattice S we shall mean that S is a meet semilattice. We shall denote the infimum of two elements a, b of S by a ∧ b, and the supremum, if it exists, by a ∨ b. A prime semilattice is a meet semilattice such that the infimum distributes over all existing finite suprema, in the sense that if x1 ∨ x2 … ∨ xn exists then (x ∧ x1) ∨ (x ∧ x2) … ∨ (x ∧ xn) exists for any x and equals x ∧ (x1 ∨ x2 … ∨ xn). Such semilattices were first studied by Balbes [1] and we use his terminology.

A non-empty subset F of S is a filter provided that x ∧ y ∊ F if and only if x ∊ F and y ∊ F.

The aim of this paper is to extend to a suitable class of topological semigroups parts of well-defined theory of representations of topological groups. In attempting to obtain these results it was soon realized that no general theory was likely to be obtainable for all locally compact semigroups. The reason for this is the absence of any analogue of the group algebra Ll(G). So the theory in this paper is restricted to a certain family of topological semigroups. In this account we shall only give the details of those parts of proofs which depart from the standard proofs of analogous theorems for groups.

On a locally compact semigroup S the algebra of all μ ∊ M(S) for which the mapping and of S to M(S) (where denotes the point mass at x) are continuous when M(S) has the weak topology was first studied in the sequence of papers [1, 2, 3] by A. C. and J. W. Baker.

Let D be a bounded domain in the Euclidean space RN(N ≦ 2) and let where is the closure of D. We assume that the boundary ∂G of G is smooth. Consider the boundary value problem (abbreviated to BVP in the sequel).

(1)

(1)

where A is a nonlinear elliptic differential operator in divergence form of Leray-Lions type, ∇u = grad u, f is a distribution on G and p(x, t, η) is a function defined on G × R × RN. Among other hypotheses we shall, roughly speaking, assume that p has completely unrelated growth rates in the first and the third variables. In this paper we prove the solvability of the BVP (1), (2) under the assumption that it has both an upper solution ψ and a lower solution φ with φ ≧ ψ.

For Kn = Q(ω) a real algebraic number field of degree n over Q such that

with D ∊ N, d ∊ Z, d|D2, and D2 + 4d > 0, we proved in [5] (by using the approach of Halter-Koch and Stender [6]) that if

with

then

is an independent system of units of Kn.

Let S denote the class of functions of the form

that are analytic and univalent in the unit disk Δ = {z:|z| < 1}, with S*(α) and K(α) designating the subclasses of S that are, respectively, starlike of order a and convex of order α, 0 ≦ α < 1. If f(z) and g(z) are analytic in Δ, we say that f(z) is subordinate to g(z), written f ≺ g, if there exists a Schwarz function w(z), w(0) = 0 and |w(z)| < 1 in Δ, such that f(z) = g(w(z)). A function f(z) = z + … is said to be in S*[A, B] if

(1)

and in K[A, B] if

(2)