Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T06:10:26.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebras of Analytic Operators associated with a Periodic Flow on a Von Neumann Algebra

Published online by Cambridge University Press:  20 November 2018

Baruch Solel
Baruch Solel*
Affiliation:
Dalhousie University, Halifax, Nova Scotia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a σ-finite von Neumann algebra and {σt}t∊T be a σ-weakly continuous representation of the unit circle, T, as *-automorphisms of M. Let H∞(σ) be the set of all x ∊ M such that

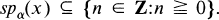
The structure of H∞(σ) was studied by several authors (see [2-13]).

The main object of this paper is to study the σ-weakly closed subalgebras of M that contain H∞(σ). In [12] this was done for the special case where H∞(σ) is a nonselfadjoint crossed product.

Let Mn, for n ∊ Z, be the set of all x ∊ M such that

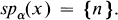
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 3 , 01 June 1985 , pp. 405 - 429
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Arveson, W. B., On groups of automorphisms of operator algebras, J. Funct. Anal. 75 (1974), 217–243.Google Scholar
2. Kawamura, S. and Tomijama, J., On subdiagonal algebras associated with flows in operator algebra, J. Math. Soc. Japan 29 (1977), 73–90.Google Scholar
3. Loebl, R. I. and Muhly, P. S., Analyticity and flows in von Neumann algebras, J. Funct. Anal. 29 (1978), 214–252.Google Scholar
4. McAsey, M., Muhly, P. S. and Saito, K.-S., Nonself adjoint crossed products (Invariant subspaces and maximality), Trans. Amer. Math. Soc. 248 (1979), 381–409.Google Scholar
5. McAsey, M., Muhly, P. S. and Saito, K.-S., Nonselfadjoint crossed products II, J. Math. Soc. Japan 33 (1981), 485–495.Google Scholar
6. McAsey, M., Muhly, P. S. and Saito, K.-S., Nons elf adjoint crossed products III (Infinite algebras), Preprint.Google Scholar
7. Saito, K.-S., The Hardy spaces associated with a periodic flow on a von Neumann algebra, Tohoku Math. J. 29 (1977), 69–75.Google Scholar
8. Saito, K.-S., Invariant subspaces for finite maximal subdiagonal algebras, Pacific J. of Math. 93 (1981), 431–434.Google Scholar
9. Saito, K.-S., Invariant subspaces and cocycles in nonself adjoint crossed products, J. Funct. Anal. 45 (1982), 177–193.Google Scholar
10. Saito, K.-S., Nonself adjoint subalgebras by compact abelian actions on finite von Neumann algebras, Tohoku Math. J. 34 (1982), 485–494.Google Scholar
11. Saito, K.-S., Spectral resolutions of invariant subspaces by compact abelian group actions on von Neumann algebras, Preprint.Google Scholar
12. Sold, B., The invariant subspace structure of Nonself adjoint crossed products, Trans. Amer. Math. Soc. 279 (1983), 825–840.Google Scholar
13. Sold, B., Invariant subspaces for algebras of analytic operators associated with a periodic flow on a finite von Neumann algebra, J. Funct. Anal. 58 (1984), 1–19.Google Scholar