Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T21:42:33.579Z Has data issue: false hasContentIssue false
  • English
  • Français

An Ergodic Theorem for Multidimensional Superadditive Processes

Published online by Cambridge University Press:  20 November 2018

Doğan Çömez
Doğan Çömez*
Affiliation:
North Dakota State University, Fargo, North Dakota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The ergodic theorem for multidimensional strongly subadditive processes relative to a semigroup 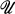induced by a measure preserving point transformation on X was proved by R. T. Smythe [18]. His results have been generalized by M. A. Akçoğlu and U. Krengel [4] to the continuous parameter case. The definition of superadditivity they used is stronger than Smythe's but weaker than strong superadditivity. R. Emilion and B. Hachem [10] extended this result to strongly superadditive processes relative to a semigroup generated by a pair of commuting Markovian operators which are also L∞-contractions. The basic tool in the proof is a technique which may be referred to as “reduction of dimension“ and they used a version of it due to A. Brunei [6].

The purpose of this paper is to show that if F = {F(uv)}u>0 is a bounded strongly superadditive process with respect to a two-dimensional strongly continuous Markovian semigroup of operators on L1, then u-2F(uu) converges a.e. as u → ∞.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 4 , 01 August 1985 , pp. 612 - 634
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Akçoğlu, M. A. and Chacon, R. V., A local ergodic theorem, Can. J. Math. 22 (1970), 545–552.Google Scholar
2. Akçoğlu, M. A. and Junco, A. del, Differentiation of n-dimensional additive processes, Can. J. Math. 33 (1981), 749–768.Google Scholar
3. Akçoğlu, M. A. and Krengel, U., A differentiation theorem for additive processes, Math. Z. 163 (1978), 199–210.Google Scholar
4. Akçoğlu, M. A. and Krengel, U., Ergodic theorems for superadditive processes, J. Reine Agnew. Math. 323 (1981), 53–67.Google Scholar
5. Akçoğlu, M. A. and Sucheston, L., A ratio ergodic theorem for superadditive processes, Z. Wahr. 44 (1978), 269–278.Google Scholar
6. Brunei, A., Théorème ergodique ponctuel pour un semigroupe commutatif finiment engendré de contractions de L1 Ann. Inst. Henri Poincaré 9 (1973), 327–343.Google Scholar
7. Chacon, R. V., A class of linear transformations, Proc. Amer. Math. Soc. 15 (1964), 560–564.Google Scholar
8. Chung, K. L., Markov chains with stationary transition probabilities, 2nd Ed. (Springer Verlag, Berlin, 1967).Google Scholar
9. Dunford, N. and Schwartz, J. T., Linear operators-I (Interscience, New York, 1958).Google Scholar
10. Emilion, R. and Hachem, B., Un théorème ergodique fortement suradditif à plusieurs paramètres, Preprint.Google Scholar
11. Hammersley, J. M. and Welsh, D. J. A., First passage percolation, subadditive processes, stochastic networks, and generalized renewal theory, Bernoulli-Laplace Anniversary Volume (Springer-Verlag, Berlin, 1965).Google Scholar
12. Hille, E. and Phillips, R. S., Functional analysis and semigroups, Collog. Publ. Amer. Math. Soc. (1957).Google Scholar
13. Hopf, E., The general temporally discrete Markov process, J. of Math, and Mech. 3 (1954), 13–45.Google Scholar
14. Kingman, J. F. C., The ergodic theory of subadditive stochastic processes, J. Roy. Stats. Soc. Ser. B 30 (1968), 499–510.Google Scholar
15. Krengel, U., A local ergodic theorem, Invent, Morth. 6 (1969), 329–333.Google Scholar
16. Kubokowa, Y., Ergodic theorems for contraction semigroups, J. Math. Soc. Japan 27 (1975), 184–193.Google Scholar
17. Sato, R., Contraction semigroups in Lebesgue space, Pacific J. Math. 78 (1978), 251–259.Google Scholar
18. Smythe, R. T., Multiparameter subadditive processes, Ann. Prob. 4 (1976), 772–782.Google Scholar
19. Terrell, T. R., Local ergodic theorems for n-parameter semigroups of operators, Contribution to Ergodic Theory and Probability, Lecture Notes in Math. 160 (Springer Verlag, Berlin, 1970), 262–278.Google Scholar