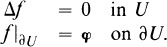Research Article
Finite Projective Planes that Admit a Strongly Irreducible Collineation Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 579-611
-
- Article
-
- You have access
- Export citation
An Ergodic Theorem for Multidimensional Superadditive Processes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 612-634
-
- Article
-
- You have access
- Export citation
Groups with Finite Dimensional Irreducible Multiplier Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 635-643
-
- Article
-
- You have access
- Export citation
An Independent System of Units in Certain Algebraic Number Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 644-663
-
- Article
-
- You have access
- Export citation
On the Definition of C*-Algebras II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 664-681
-
- Article
-
- You have access
- Export citation
Extreme Positive Contractions on Finite Dimensional lp-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 682-699
-
- Article
-
- You have access
- Export citation
Generalized L(f) Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 700-709
-
- Article
-
- You have access
- Export citation
Beyond the Enveloping Algebra of sl3
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 710-729
-
- Article
-
- You have access
- Export citation
Strongs-Sequences and Variations on Martin's Axiom
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 730-746
-
- Article
-
- You have access
- Export citation
Application of a Selection Theorem to Hyperspace Contractibility
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 747-759
-
- Article
-
- You have access
- Export citation
The Dirichlet Problem for the Subelliptic Laplacian on the Heisenberg Group II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 760-766
-
- Article
-
- You have access
- Export citation
Correction
A Correction to: Discrete Open and Closed Mappings on Generalized Continua and Newman's Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 767-768
-
- Article
-
- You have access
- Export citation

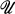 induced by a measure preserving point transformation on
induced by a measure preserving point transformation on 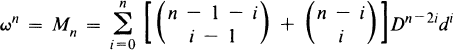
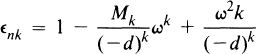
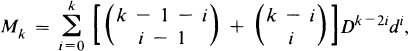

 with
with 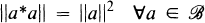
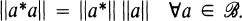
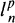 are strongly exposed.
are strongly exposed.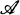 ,
, 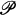 be the family of all finite subsets of
be the family of all finite subsets of 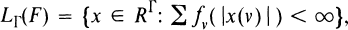
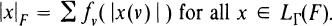
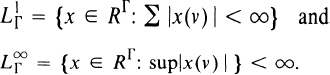
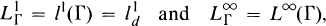
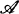 a pairwise disjoint family of sets and a subset of each member of
a pairwise disjoint family of sets and a subset of each member of  there exists
there exists 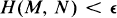 .
.