Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Charatonik, Włodzimierz J.
1986.
Ri-continua and hyperspaces.
Topology and its Applications,
Vol. 23,
Issue. 3,
p.
207.
Artstein, Zvi
and
Prikry, Karel
1987.
Caratheodory selections and the Scorza Dragoni property.
Journal of Mathematical Analysis and Applications,
Vol. 127,
Issue. 2,
p.
540.
Borisovich, Yu. G.
Gel'man, B. D.
Myshkis, A. D.
and
Obukhovskii, V. V.
1990.
New results in the theory of multivalued mappings. I. Topological characteristics and solvability of operator relations.
Journal of Soviet Mathematics,
Vol. 49,
Issue. 1,
p.
800.
van de Vel, M.
1991.
Invariant arcs, Whitney levels, and Kelley continua.
Transactions of the American Mathematical Society,
Vol. 326,
Issue. 2,
p.
749.
Zarichnyi, M. M.
and
Fedorchuk, V. V.
1991.
Covariant functors in categories of topological spaces.
Journal of Soviet Mathematics,
Vol. 53,
Issue. 2,
p.
147.
Kato, Hisao
1991.
A note on continuous mappings and the property of J. L. Kelley.
Proceedings of the American Mathematical Society,
Vol. 112,
Issue. 4,
p.
1143.
Lynch, Mark
1991.
Whitney levels and certain order arc spaces.
Topology and its Applications,
Vol. 38,
Issue. 2,
p.
189.
van de Vel, M.
1993.
A selection theorem for topological convex structures.
Transactions of the American Mathematical Society,
Vol. 336,
Issue. 2,
p.
463.
Repovš, D.
Semenov, P.V.
and
Ščepin, E.V.
1993.
On zero-dimensional Milutin maps and Michael selection theorems.
Topology and its Applications,
Vol. 54,
Issue. 1-3,
p.
77.
1993.
Theory of Convex Structures.
Vol. 50,
Issue. ,
p.
507.
Rhee, Choon Jai
1995.
Admissible fibers and T-admissibility in hyperspaces.
Topology and its Applications,
Vol. 64,
Issue. 1,
p.
75.
Li, Lei
and
Wu, Congxin
1997.
Continuous selections for pseudo-lower semicontinuous set-valued mappings on convex structure spaces and hyperspace contractibility.
Chinese Science Bulletin,
Vol. 42,
Issue. 14,
p.
1230.
Charatonik, Janusz J.
1998.
Handbook of the History of General Topology.
Vol. 2,
Issue. ,
p.
703.
Semenov, P. V.
2000.
Nonconvexity in problems of multivalued calculus.
Journal of Mathematical Sciences,
Vol. 100,
Issue. 6,
p.
2682.
Repovš, Dušan
and
Semenov, Pavel V.
2002.
Recent Progress in General Topology II.
p.
423.
Michael, E.
2003.
Encyclopedia of General Topology.
p.
107.
Chacón-Tirado, Mauricio
2017.
Hyperspaces of maximal order arcs.
Topology and its Applications,
Vol. 221,
Issue. ,
p.
412.
Camargo, Javier
Maya, David
and
Pellicer-Covarrubias, Patricia
2022.
Noncut subsets of the hyperspace of subcontinua.
Topology and its Applications,
Vol. 305,
Issue. ,
p.
107867.
 there exists δ > 0 such that, for every pair of points x, y with d(x, y) < δ and every subcontinuum M containing x, there exists a subcontinuum N containing y with
there exists δ > 0 such that, for every pair of points x, y with d(x, y) < δ and every subcontinuum M containing x, there exists a subcontinuum N containing y with 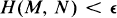 .
.

