Article contents
Strongs-Sequences and Variations on Martin's Axiom
Published online by Cambridge University Press: 20 November 2018
Extract
As part of their study of βω — ω and βω1 — ω1, A. Szymanski and H. X. Zhou [3] were able to exploit the following difference between ω, and ω: ω1, contains uncountably many disjoint sets whereas any uncountable family of subsets of ω is, at best, almost disjoint. To translate this distinction between ω1, and ω to a possible distinction between βω1 — ω1, and βω — ω they used the fact that if 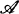 a pairwise disjoint family of sets and a subset of each member of
a pairwise disjoint family of sets and a subset of each member of 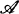 is chosen then it is trivial to find a single set whose intersection with each member
is chosen then it is trivial to find a single set whose intersection with each member 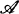 is the chosen set. However, they noticed, it is not clear that the same is true if
is the chosen set. However, they noticed, it is not clear that the same is true if 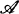 is only a pairwise almost disjoint family even if we only require equality except on a finite set. But any homeomorphism from βω1 — ω1 to βω — ω would have to carry a disjoint family of subsets of ω1, to an almost disjoint family of subsets of ω with this property. This observation should motivate the following definition.
is only a pairwise almost disjoint family even if we only require equality except on a finite set. But any homeomorphism from βω1 — ω1 to βω — ω would have to carry a disjoint family of subsets of ω1, to an almost disjoint family of subsets of ω with this property. This observation should motivate the following definition.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1985
References
- 9
- Cited by


