Article contents
On the Definition of C*-Algebras II
Published online by Cambridge University Press: 20 November 2018
Extract
The theory of noncommutative involutive Banach algebras (briefly Banach *-algebras) owes its origin to Gelfand and Naimark, who proved in 1943 the fundamental representation theorem that a Banach *-algebra 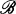 with C*-condition
with C*-condition
(C*)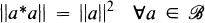
is *-isomorphic and isometric to a norm-closed self-adjoint subalgebra of all bounded operators on a suitable Hilbert space.
At the same time they conjectured that the C*-condition can be replaced by the B*-condition.
(B*)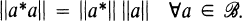
In other words any B*-algebra is actually a C*-algebra. This was shown by Glimm and Kadison [5] in 1960.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1985
References
- 3
- Cited by


