Research Article
Alternative quasialgebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 257-268
-
- Article
-
- You have access
- Export citation
The dyadic trace and odd weight computations for Siegel modular cusp forms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 269-271
-
- Article
-
- You have access
- Export citation
A Bryce and Cossey type theorem in a class of locally finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 459-466
-
- Article
-
- You have access
- Export citation
A note on the circle actions on Einstein manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-91
-
- Article
-
- You have access
- Export citation
Restricted weak upper semicontinuous differentials of convex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 93-100
-
- Article
-
- You have access
- Export citation
A useful lemma concerning subseries convergence
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-277
-
- Article
-
- You have access
- Export citation
Polynomial representations of the Diffie-Hellman mapping
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 467-473
-
- Article
-
- You have access
- Export citation
An extension of Jensen's form
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-298
-
- Article
-
- You have access
- Export citation
A metrisation theorem for pseudocompact spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-104
-
- Article
-
- You have access
- Export citation
Isometries of spaces of unbounded continuous functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 475-484
-
- Article
-
- You have access
- Export citation
Some new generalisations of inequalities of Hardy and Levin–Cochran–Lee
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 105-113
-
- Article
-
- You have access
- Export citation
An extension of the Grünwald–Marcinkiewicz interpolation theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-320
-
- Article
-
- You have access
- Export citation
On the existence of Chapman-Jouguet detonation waves
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 485-496
-
- Article
-
- You have access
- Export citation
Some New Poincaré-type inequalities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-327
-
- Article
-
- You have access
- Export citation
Diffusion approximation for a Knudsen gas in a thin domain with reflexive chaotic law
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 497-514
-
- Article
-
- You have access
- Export citation
On (k, l)-sets in cyclic groups of odd prime order
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 115-121
-
- Article
-
- You have access
- Export citation
Nonuniqueness and wellposedness of abstract Cauchy problems in a Fréchet space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 123-131
-
- Article
-
- You have access
- Export citation
Classifying a family of symmetric graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-335
-
- Article
-
- You have access
- Export citation
Poisson manifolds in generalised Hamiltonian biomechanics
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 515-526
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Integrability of strongly correlated electron systems on open chains
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 527-528
-
- Article
-
- You have access
- Export citation

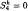 for odd
for odd 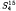 ≤ 4.
≤ 4.