Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T14:44:06.276Z Has data issue: false hasContentIssue false
  • English
  • Français

The dyadic trace and odd weight computations for Siegel modular cusp forms

Published online by Cambridge University Press:  17 April 2009

Cris Poor  and
David S. Yuen
Cris Poor
Affiliation:
Department of Mathematics, Fordham University, Bronx, NY 10458, e-mail: [email protected]
David S. Yuen
Affiliation:
Math. and Computer Science Department, Lake Forest College, 555 N. Sheridan Rd., Lake Forest, IL 60045, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define the concept of a special positive matrix. We use the dyadic trace to prove the result that dim 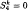for odd k ≤ 13 and that dim 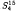≤ 4.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 63 , Issue 2 , April 2001 , pp. 269 - 271
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Freitag, E., Siegelsche modulfunktionen, Grundlehren der Mathematische Wissenschaften 254 (Springer-Verlag, Berlin, Heidelberg, New York, 1983).CrossRefGoogle Scholar
[2]Klingen, H., Introductory lectures on Siegel modular forms, Cambridge Studies in Advanced Mathematics 20 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
[3]Nipp, G., Quaternary quadratic forms, computer generated tables (Springer-Verlag, Berlin, Heidelbrg, New York).Google Scholar
[4]Poor, C. and Yuen, D., ‘Dimensions of spaces of Siegel modular forms of low weight in degree four’, Bull. Austral. Math. Soc. 54 (1996), 309–315.CrossRefGoogle Scholar
[5]Poor, C. and Yuen, D., ‘Linear dependence among Siegel modular forms’, Math. Ann. 318 (2000), 205–234.CrossRefGoogle Scholar