Research Article
Relationships between widths of a convex body and of an inscribed parallelotope
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 133-140
-
- Article
-
- You have access
- Export citation
A simple proof of the sum formula
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-339
-
- Article
-
- You have access
- Export citation
Dimension invariance of subdivisions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 141-150
-
- Article
-
- You have access
- Export citation
Power graphs and semigroups of matrices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 341-344
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 63 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Research Article
Large deviation results for a U-statistical sum with product kernel
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-165
-
- Article
-
- You have access
- Export citation
Corrigendum
Finding common fixed points of nonexpansive mappings by iteration: Corrigendum
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 345-346
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 63 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
On diagonal acts of monoids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 167-175
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Finite irreducible monomial groups of small prime degree
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 347-348
-
- Article
-
- You have access
- Export citation
Codes and arrays from cocycles
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 349-350
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 63 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 63 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Some results on the derived series of finite p-groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 351-352
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 63 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 63 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

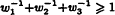 , where
, where 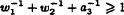 , where
, where 