Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bronstein, E. M.
2008.
Approximation of convex sets by polytopes.
Journal of Mathematical Sciences,
Vol. 153,
Issue. 6,
p.
727.
Nevskii, M. V.
2015.
On Some Results in the Geometry of Convex Bodies and their Applications.
Modeling and Analysis of Information Systems,
Vol. 19,
Issue. 3,
p.
113.


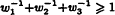 , where
, where 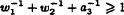 , where
, where 