Research Article
Lambek's operational categories
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-175
-
- Article
-
- You have access
- Export citation
Symmetry groups on ordered Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-187
-
- Article
-
- You have access
- Export citation
Extensions of Jensen's inequality on the unit circle
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 189-194
-
- Article
-
- You have access
- Export citation
Frenet formulae for holomorphic curves in the two quadric
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 195-206
-
- Article
-
- You have access
- Export citation
A link between Lebesgue constants and Hermite-Fejér interpolation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 207-218
-
- Article
-
- You have access
- Export citation
Fields countably generated over a proper subfield
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 219-226
-
- Article
-
- You have access
- Export citation
On adjoints of non-linear mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 227-236
-
- Article
-
- You have access
- Export citation
A preemptive priority queue with a general bulk service rule
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 237-243
-
- Article
-
- You have access
- Export citation
Simple groups of small Engel depth
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 245-251
-
- Article
-
- You have access
- Export citation
A note on the coefficients of mixed normed spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 253-260
-
- Article
-
- You have access
- Export citation
The semidirect product of an inverse semigroup and a group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 261-272
-
- Article
-
- You have access
- Export citation
A note on compact subgroups of topological groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-278
-
- Article
-
- You have access
- Export citation
A note on containment of operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-291
-
- Article
-
- You have access
- Export citation
On a property of ideals of differentiable functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-305
-
- Article
-
- You have access
- Export citation
Weighted function algebras on groups and semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-318
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
The numerical solution of second kind Fredholm integral equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 319-320
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 33 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 33 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

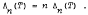
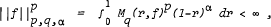
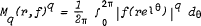
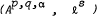
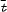
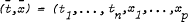 which does not depend on
which does not depend on 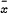
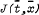 . Consider the following statement (1) on
. Consider the following statement (1) on 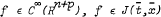 if and only if for every fixed
if and only if for every fixed 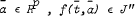 .
.