Research Article
On strongly right bounded finite rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-355
-
- Article
-
- You have access
- Export citation
The centraliser of the injective tensor product
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-365
-
- Article
-
- You have access
- Export citation
On direct bifurcations into chaos and order for a simple family of interval maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-373
-
- Article
-
- You have access
- Export citation
Local integrability of CR-hypersurfaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 375-380
-
- Article
-
- You have access
- Export citation
Non-isomorphic 2-perfect 6-cycle systems of order 13
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 381-385
-
- Article
-
- You have access
- Export citation
A commutativity theorem for rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-389
-
- Article
-
- You have access
- Export citation
Finite type pseudo-umbilical submanifolds in a hypersphere
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-396
-
- Article
-
- You have access
- Export citation
Local minima of the Gauss curvature of a minimal surface
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 397-404
-
- Article
-
- You have access
- Export citation
Minimal partial clones
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-415
-
- Article
-
- You have access
- Export citation
The primes of S(R)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 417-427
-
- Article
-
- You have access
- Export citation
Small squaring and cubing properties for finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-450
-
- Article
-
- You have access
- Export citation
Extensions of certain results in Walsh-type equiconvergence
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 451-460
-
- Article
-
- You have access
- Export citation
The sup metric on infinite products
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 461-466
-
- Article
-
- You have access
- Export citation
Existence of solutions of nonlinear differential equations with deviating arguments
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 467-476
-
- Article
-
- You have access
- Export citation
A result concerning additive maps on the set of quaternions and an application
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-482
-
- Article
-
- You have access
- Export citation
Holomorphic curves in the orthogonal twistor space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 483-499
-
- Article
-
- You have access
- Export citation
Duality in nonconvex vector minimum problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 501-509
-
- Article
-
- You have access
- Export citation
Quadratic systems with a weak focus
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 511-526
-
- Article
-
- You have access
- Export citation
A remark on boundedness of Bloch functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 527-528
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 44 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation

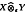 ). More precisely, we are going to prove that
). More precisely, we are going to prove that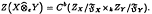
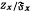 and
and 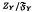 depend only on
depend only on 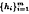 from
from 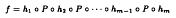
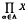
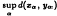 , is the sup metric on
, is the sup metric on  |
|