Article contents
The primes of S(R)
Published online by Cambridge University Press: 17 April 2009
Abstract
S(R) is the semigroup, under composition, of all continuous selfmaps of the space R of real numbers. We show that the primes of S(R) are precisely those continuous selfmaps which are surjective and have exactly two local extrema. Additional results are then derived from this. For example, if f is any surjective continuous selfmap of R with n ≥ 2 local extrema, then there exist homeomorphisms 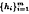 from R onto R such that m ≤ 1 + n/2 and
from R onto R such that m ≤ 1 + n/2 and
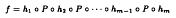
where P is the polynomial defined by P(x) = x3 − x. It follows from this that the homeomorphisms together with the polynomial P generate a dense subsemigroup of S(R) where the topology on S(R) is the compact-open topology.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 44 , Issue 3 , December 1991 , pp. 417 - 427
- Copyright
- Copyright © Australian Mathematical Society 1991
References
- 1
- Cited by


