In this paper, Antczak's η-approximation approach is used to prove the equivalence between optima of multiobjective programming problems and the η-saddle points of the associated η-approximated vector optimisation problems. We introduce an η-Lagrange function for a constructed η-approximated vector optimisation problem and present some modified η-saddle point results. Furthermore, we construct an η-approximated Mond-Weir dual problem associated with the original dual problem of the considered multiobjective programming problem. Using duality theorems between η-approximation vector optimisation problems and their duals (that is, an η-approximated dual problem), various duality theorems are established for the original multiobjective programming problem and its original Mond-Weir dual problem.

We analyse an optimal portfolio and consumption problem with stochastic factor and delay over a finite time horizon. The financial market includes a risk-free asset, a risky asset and a stochastic factor. The price process of the risky asset is modelled as a stochastic differential delay equation whose coefficients vary according to the stochastic factor; the drift also depends on its historical performance. Employing the stochastic dynamic programming approach, we establish the associated Hamilton–Jacobi–Bellman equation. Then we solve the optimal investment and consumption strategies for the power utility function. We also consider a special case in which the price process of the stochastic factor degenerates into a Cox–Ingersoll–Ross model. Finally, the effects of the delay variable on the optimal strategies are discussed and some numerical examples are presented to illustrate the results.

This paper concerns a nonlinear doubly degenerate reaction–diffusion equation which appears in a bacterial growth model and is also of considerable mathematical interest. A travelling wave analysis for the equation is carried out. In particular, the qualitative behaviour of both sharp and smooth travelling wave solutions is analysed. This travelling wave behaviour is also verified by some numerical computations for a special case.

This paper discusses robust stochastic stability and stabilization of time-delay discrete Markovian jump singular systems with parameter uncertainties. Based on the restricted system equivalent (RES) transformation, a delay-dependent linear matrix inequalities condition for time-delay discrete-time Markovian jump singular systems to be regular, causal and stochastically stable is established. With this condition, problems of robust stochastic stability and stabilization are solved, and delay-dependent linear matrix inequalities are obtained. A numerical example is also given to illustrate the effectiveness of this method.2000Mathematics subject classification: primary 39A12; secondary 93C55.

This note describes a simple numerical method for solution of the lifting surface integral equation of aerodynamics, and provides benchmark computations of up to 7 figure accuracy for flat rectangular wings of arbitrary aspect ratio. The nature of the large aspect ratio limit is also investigated numerically and asymptotically. This enables determination of the limiting behaviour near the wing tips, which is compared to the predictions of lifting line theory. Generalisations to non-rectangular wings are discussed.

Solitary wave interaction is examined using an extended Benjamin-Bona-Mahony (eBBM) equation. This equation includes higher-order nonlinear and dispersive effects and is is asymptotically equivalent to the extended Korteweg-de Vries (eKdV) equation. The eBBM formulation is preferable to the eKdV equation for the numerical modelling of solitary wave collisions, due to the stability of its finite-difference scheme. In particular, it allows the interaction of steep waves to be modelled, which due to numerical instability, is not possible using the eKdV equation.

Numerical simulations of a number of solitary wave collisions of varying nonlinearity are performed for two special cases corresponding to surface water waves. The mass and energy of the dispersive wavetrain generated by the inelastic collision is tabulated and used to show that the change in solitary wave amplitude after interaction is of O(α4), verifying previously obtained theoretical predictions.

A substance carried convectively through the liver by the blood undergoes two successive enzymatic transformations. The resulting concentrations of the three forms of the substance are determined, as functions of position along the blood flow in the steady state, by coupled ordinary differential equations of the first order on a finite interval. The densities along the blood flow of the activities of the two (immobile) transforming enzymes are described by two non-negative and normalised functions of position.

The problem, suggested by recent experimental results, is to choose these two functions so as to minimise the concentration of the once-transformed (intermediate) form of the substance at one boundary (the liver outlet). That minimisation is particularly significant biologically when the intermediate form is toxic and the second transformation renders it harmless. In this problem of optimal control (exerted perhaps by natural selection), the classical approach through Euler's equations is inapplicable because of the constraints on the two density functions. Moreover, when the enzyme kinetics and hence the differential equations are non-linear, the functional to be minimised is not obtainable explicitly. Instead it appears, after some manipulation of the coupled equations, as the terminal boundary value of the solution of a non-linear Volterra integral equation, which involves the two density functions (one explicitly and one implicitly) as control variables.

Appropriate existence, uniqueness and boundedness results are obtained for the solution of this integral equation, and the problem is then solved rigorously for one class of non-linearities (including saturation kinetics). Some unanswered questions are posed for another class (including substrate-inhibition kinetics).

Given the data (pi, ti, fi), i = 1,…,m, we consider the existence problem for the best least squares approximation of parameters for the 3-parametric exponential regression model. This problem does not always have a solution. In this paper it is shown that this problem has a solution provided that the data are strongly increasing at the ends.

The most fundamental characteristic of a physical system can often be deduced from its behaviour under discrete symmetry transformations, such as time reversal, parity and chirality. Here, we review some of the basic symmetry properties of the relativistic quantum theories for free electrons in ($2+1$)- and ($1+1$)-dimensional spacetime. Additional flavour degrees of freedom are necessary to properly define symmetry operations in ($2+1$) dimensions, and are generally present in physical realizations of such systems, for example in single sheets of graphite. We find that there exist two possibilities for defining any flavour-coupling discrete symmetry operation of the two-flavour ($2+1$)-dimensional Dirac theory. Some physical implications of this previously unnoticed duplicity are discussed.

We investigate two routing problems that arise when order pickers traverse an aisle in a warehouse. The routing problems can be viewed as Euclidean travelling salesman problems with points on two parallel lines. We show that if the order picker traverses only a section of the aisle and then returns, then an optimal solution can be found in linear time, and if the order picker traverses the entire aisle, then an optimal solution can be found in quadratic time. Moreover, we show how to approximate the routing cost in linear time by computing a minimum spanning tree for the points on the parallel lines.

A boundary integral equation of the first kind is discretised using Galerkin's method with piecewise-constant trial functions. We show how the condition number of the stiffness matrix depends on the number of degrees of freedom and on the global mesh ratio. We also show that diagonal scaling eliminates the latter dependence. Numerical experiments confirm the theory, and demonstrate that in practical computations involving strong local mesh refinement, diagonal scaling dramatically improves the conditioning of the Galerkin equations.

A class of optimal control models which involve different weightings in the integrand of the objective function is considered. The motivation for considering this class of problems is that this type of objective function is used to account for eccentric movement in biomechanical models. The computation of these optimal control problems using control parametrization directly is difficult, firstly because of ill-conditioning, and secondly because the objective function is not differentiable. A method for smoothing the integrand is presented with convergence results. An example is computed which shows favourable computational improvements.

A five-dimensional deterministic model is proposed for the dynamics between HIV and another pathogen within a given population. The model exhibits four equilibria: a disease-free equilibrium, an HIV-free equilibrium, a pathogen-free equilibrium and a co-existence equilibrium. The existence and stability of these equilibria are investigated. A competitive finite-difference method is constructed for the solution of the non-linear model. The model predicts the optimal therapy level needed to eradicate both diseases.

A model is presented for describing the propagation of a one-dimensional wave of permanent form in a compressible gas in a pipe. Energy is lost to the system through the walls of the pipe, but the combustion wave produces heat through an exothermic chemical reaction. The full set of equations for the model is reduced to a phase-plane system, and it is shown that, for small amplitude waves, a weakly non-linear analysis leads to a temperature profile that is a classical solitary wave. A novel shooting method is developed for the full non-linear problem, and this confirms and extends the solitary-wave solution, up to a value of the temperature amplitude at which the wave begins to develop a shock. The jump conditions across the shock are presented, and numerical integration is used to continue the solution for temperature amplitudes at which a shock is present. An example is given of the extreme situation in which the shock is so strong that all the fuel behind the shock is exhausted.

A linear programming model for optimally assigning diameters to a gas pipeline network is discussed. Computational results for a real life situation are presented, and certain properties that have to be satisfied by an optimal assignment are derived.

Consider the forced differential equation with variable delay

where

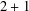
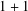
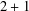
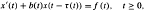
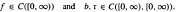
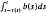We establish a sufficient condition for every solution to tend to zero. We also obtain a sharper condition for every solution to tend to zero when is asymptotically constant.

We give sufficient conditions for order-bounded convex operators to be generically differentiable (Gâteaux or Fréchet). When the range space is a countably order-complete Banach lattice, these conditions are also necessary. In particular, every order-bounded convex operator from an Asplund space into such a lattice is generically Fréchet differentiable, if and only if the lattice has weakly-compact order intervals, if and only if the lattice has strongly-exposed order intervals. Applications are given which indicate how such results relate to optimization theory.

In this paper, an efficient computation method is developed for solving a general class of minmax optimal control problems, where the minimum deviation from the violation of the continuous state inequality constraints is maximized. The constraint transcription method is used to construct a smooth approximate function for each of the continuous state inequality constraints. We then obtain an approximate optimal control problem with the integral of the summation of these smooth approximate functions as its cost function. A necessary condition and a sufficient condition are derived showing the relationship between the original problem and the smooth approximate problem. We then construct a violation function from the solution of the smooth approximate optimal control problem and the original continuous state inequality constraints in such a way that the optimal control of the minmax problem is equivalent to the largest root of the violation function, and hence can be solved by the bisection search method. The control parametrization and a time scaling transform are applied to these optimal control problems. We then consider two practical problems: the obstacle avoidance optimal control problem and the abort landing of an aircraft in a windshear downburst.

Line distributions of Stokes flow singularities are used to model the flow around a slender body which is straddling a flat interface between two viscous fluids. Motion of the slender body parallel to the interface and normal to the interface is considered where the axis of symmetry of the slender body is always perpendicular to the undisturbed interface. Asymptotic approximations to the force distributions on the slender body are evaluated and the relative contributions of that part of the slender body in one fluid to the force distribution in the other fluid and of the interface interaction to the force distribution are examined. It is observed that a shielding region exists about the interface which is due to the interaction with that part of the slender body in the other fluid. Finally, for parallel motion, the first order interface deformation is calculated.

Random networks were first used to model epidemic dynamics in the 1950s, but in the last decade it has been realized that scale-free networks more accurately represent the network structure of many real-world situations. Here we give an analytical and a Monte Carlo method for approximating the basic reproduction number ${R}_{0} $ of an infectious agent on a network. We investigate how final epidemic size depends on ${R}_{0} $ and on network density in random networks and in scale-free networks with a Pareto exponent of 3. Our results show that: (i) an epidemic on a random network has the same average final size as an epidemic in a well-mixed population with the same value of ${R}_{0} $; (ii) an epidemic on a scale-free network has a larger average final size than in an equivalent well-mixed population if ${R}_{0} \lt 1$, and a smaller average final size than in a well-mixed population if ${R}_{0} \gt 1$; (iii) an epidemic on a scale-free network spreads more rapidly than an epidemic on a random network or in a well-mixed population.