We show that for any 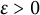 $\varepsilon>0$, the number of monic, reciprocal, length-
$\varepsilon>0$, the number of monic, reciprocal, length-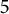 $5$ integer polynomials that have house at least
$5$ integer polynomials that have house at least 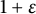 $1+\varepsilon $ is finite. The proof is algorithmic, and we are consequently able to compute a complete list (not imposing any bound on the degree) of small Mahler measures of length-
$1+\varepsilon $ is finite. The proof is algorithmic, and we are consequently able to compute a complete list (not imposing any bound on the degree) of small Mahler measures of length-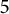 $5$ polynomials that have house at least
$5$ polynomials that have house at least 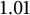 $1.01$.
$1.01$.
For larger lengths, the analogous finiteness statement is false, as we show by examples. For length 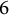 $6$ we show that if one also imposes an upper bound for the Mahler measure that is strictly below the smallest Pisot number
$6$ we show that if one also imposes an upper bound for the Mahler measure that is strictly below the smallest Pisot number 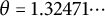 $\theta = 1.32471\cdots $, and if the length
$\theta = 1.32471\cdots $, and if the length 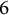 $6$ polynomial is a cyclotomic multiple of an irreducible polynomial, then the number of polynomials with house at least
$6$ polynomial is a cyclotomic multiple of an irreducible polynomial, then the number of polynomials with house at least 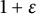 $1+\varepsilon $ is finite.
$1+\varepsilon $ is finite.
We pursue these ideas to search opportunistically for small Mahler measures represented by longer polynomials. We find one new small measure.
We give an algorithm that finds all Salem numbers in an interval 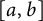 $[a,b]$ that are the Mahler measure of an integer polynomial of length at most
$[a,b]$ that are the Mahler measure of an integer polynomial of length at most 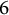 $6$, provided
$6$, provided 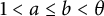 $1<a \le b < \theta $.
$1<a \le b < \theta $.