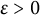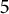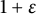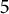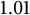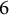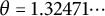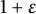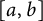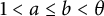Small Mahler measures with bounds on the house and shortness

Abstract

We show that for any $\varepsilon>0$, the number of monic, reciprocal, length-$5$ integer polynomials that have house at least $1+\varepsilon $ is finite. The proof is algorithmic, and we are consequently able to compute a complete list (not imposing any bound on the degree) of small Mahler measures of length-$5$ polynomials that have house at least $1.01$.

For larger lengths, the analogous finiteness statement is false, as we show by examples. For length $6$ we show that if one also imposes an upper bound for the Mahler measure that is strictly below the smallest Pisot number $\theta = 1.32471\cdots $, and if the length $6$ polynomial is a cyclotomic multiple of an irreducible polynomial, then the number of polynomials with house at least $1+\varepsilon $ is finite.

We pursue these ideas to search opportunistically for small Mahler measures represented by longer polynomials. We find one new small measure.

We give an algorithm that finds all Salem numbers in an interval $[a,b]$ that are the Mahler measure of an integer polynomial of length at most $6$, provided $1<a \le b < \theta $.

1 Introduction

Since 1933, when Lehmer [10] posed the question as to whether or not there is a gap in the spectrum of Mahler measures greater than $1$ for polynomials that have integer coefficients, many computations have been done to find small Mahler measures, providing some evidence that the answer to Lehmer’s question might be ‘yes’, and that the example $1.17628\cdots $ found by Lehmer might even be the smallest that is greater than $1$ . Early searches [2, 3] took $1.3$ as a measure of smallness, as this is slightly smaller than the smallest Pisot number ( $1.32471\cdots $ ), and to some extent this notion of ‘small’ has stuck. Notably, Mossinghoff [13] found more than 8000 ‘small’ (less than $1.3$ ) Mahler measures that have degree at most 180. The heuristic technique used was to restrict to polynomials of height $1$ (the height being the largest modulus of any coefficient) and small length (the sum of the moduli of the coefficients). Since there are limit points of the set of Mahler measures that lie below 1.3, one has to set a degree bound here if there is to be a challenge to the task of finding ‘small’ measures, else one could simply take a sequence of measures approaching a limit point below 1.3 and produce as many as one pleases. The overwhelming majority of the known small Mahler measures are members of sequences known to converge to these limit points. The smallest such limit point known is $1.25543\cdots $ , and this has prompted the suggestion that $1.25$ might be a better measure of smallness. So as not to abandon tradition entirely, we shall use ‘tiny’ to indicate a Mahler measure in the interval $(1,1.25]$ , and ‘small’ for the interval $(1,1.3]$ . There are $236$ known tiny Mahler measures; the total number is plausibly finite, and perhaps the known list of $236$ is complete. When searching for tiny Mahler measures, one does not a priori bound the degree, as there are no known tiny limit points.

Some measures have been added to Mossinghoff’s 1998 list: Lisonek, like Mossinghoff, searched for sparse polynomials; Rhin and Sac-Épée [15] used a numerical descent technique; Mossinghoff, Pinner, and Vaaler [12], and also Rhin and Sac-Épée [15] generated polynomials that were ‘close’ to being cyclotomic (a cyclotomic polynomial means a monic integer polynomial all of whose zeros are roots of unity); Boyd and Mossinghoff [4], and also El Otmani, Maul, Rhin and Sac-Épée [8], tested polynomials associated with limit points, and the latter paper also found $2$ examples by a genetic algorithm. Most recently, in an attempt to ‘explain’ these small Mahler measures combinatorially [6], a single new example was found.

For degrees up to $44$ , the lists of known small Mahler measures are provably complete [14]. In this paper we establish some completeness results relative to different measures of size: the house and (reciprocal or cyclotomic) shortness of an algebraic number (definitions to follow in Section 2).

We are able to show that if the house is at least $1.01$ , and the shortness is $5$ , then the list of known small Mahler measures is complete. For shortness $6$ , we use explicit Rouché estimates to show that the known list of small Mahler measures is complete subject to the house being at least $1.17$ . We push this bound down to $1.01$ with the further restriction that the short polynomial has degree at most $512$ , and with a bound of $180$ for the degree of the noncyclotomic part. For larger values of the shortness, we employed a heuristic search; the results are no longer complete, but we did find a new small Mahler measure.

For cyclotomic shortness at most $6$ , we give an algorithm to find all Salem numbers in an interval $[a,b]$ , where $1<a\le b < \theta $ , where $\theta = 1.32\cdots $ is the real root of $z^3-z-1=0$ .

2 House, length and Mahler measure

We start by recalling and illustrating some definitions, and then we will state the main results.

For $P(z)$ a nonzero polynomial with complex coefficients, we can write

$$\begin{align*}P(z) = a\prod_{j=1}^d(z - \alpha_j)\,,\end{align*}$$

where d is the degree of $P(z)$ , $a\ne 0$ , and $\alpha _1$ , …, $\alpha _d$ are the zeros of $P(z)$ . Then the Mahler measure of $P(z)$ , which we denote $M(P)$ , is defined by

(2.1) $$ \begin{align} M(P) = |a|\prod_{j=1}^d \max(1, |\alpha_j|)\,. \end{align} $$

Restricting to polynomials $P(z)$ having coefficients in $\mathbb {Z}$ , Lehmer’s question asks about ‘small’ Mahler measures greater than $1$ . We make this more precise by defining the Mahler measure of $P(z)\in \mathbb {Z}[z]$ to be small if it is below 1.3. As mentioned in the introduction, this is consistent with historical searches for ‘small’ Mahler measures. If the Mahler measure is below 1.25, then we declare it to be tiny.

From (2.1), we see that if the Mahler measure of $P(z)\in \mathbb {Z}[z]$ is to be small, let alone tiny, then $P(z)$ must be monic: henceforth we make this restriction on P. Then $M(P)$ is simply the product of the absolute values of those zeros of $P(z)$ that lie outside the unit disc. The zeros of such polynomials are algebraic integers. By a theorem of Smyth [17] (and for a less precise version, see [5]), if the Mahler measure of $P(z)$ is small, then $P(z)$ must be reciprocal (meaning that $z^{\deg (P)} P(1/z) = \pm P(z)$ ). We therefore restrict our attention to monic reciprocal polynomials $P(z)\in \mathbb {Z}[z]$ .

The house of an algebraic integer $\alpha $ is the maximum modulus of its conjugates. We write for the house of $\alpha $ . More generally, the house of a polynomial $P(z)\in \mathbb {Z}[z]$ , is the largest modulus of any of its zeros. There is no requirement here that P is irreducible. We see that the house of an algebraic integer equals the house of its minimal polynomial. If an algebraic integer is not a root of unity, then its house is greater than $1$ by Kronecker’s Theorem [11, Theorem 1.3]. We write $M(\alpha )$ for the Mahler measure of the minimal polynomial of $\alpha $ , and we note that trivially , with equality if and only $\alpha $ has precisely one conjugate outside the unit disc.

The length of a polynomial $P(z) = \sum _{i=0}^d a_iz^i \in \mathbb {Z}[z]$ is simply the sum of the absolute values of the coefficients, $|a_0| + \cdots + |a_d|$ . It might be that there is some $T(z)\in \mathbb {Z}[z]$ for which the length of $P(z)T(z)$ is less than that of $P(z)$ . Indeed for all small Mahler measures known, the minimal polynomial $P(z)$ has some multiple that has length at most $14$ [13, p. 1703], and the majority have a polynomial multiple that has length only $5$ . If we wish to preserve Mahler measure, then we should restrict $T(z)$ to being cyclotomic, but methods for seeking short multiples might be more general. (Recall from the introduction that a cyclotomic polynomial is a monic integer polynomial all of whose zeros are roots of unity. There is no requirement that a cyclotomic polynomial be irreducible, or squarefree.) In [11, Section 1.7], the ‘shortness’ of a polynomial $P(z)$ is defined as the smallest length of $P(z)T(z)$ where $T(z)$ is cyclotomic. For this paper we shall call this the cyclotomic shortness of $P(z)$ (or shortness for short, as in [11]). By a result of Dobrowolski [7, Corollary 2], one can in principle compute the shortness of any polynomial, but as noted in the concluding sentences of that paper, this approach is completely impractical. Our attempts to compute the cyclotomic shortness of $P(z)$ will in practice consider multiplying $P(z)$ by a polynomial $T(z)$ that is not a priori cyclotomic (and perhaps not even a posteriori!), but where instead $T(z)$ is a monic reciprocal polynomial. We call the shortest multiple of $P(z)$ by a monic reciprocal polynomial the reciprocal shortness of $P(z)$ , to distinguish this from the (cyclotomic) shortness.

One readily checks that all really short monic reciprocal polynomials are cyclotomic, and record this as a Remark.

Remark 2.1 If a monic reciprocal polynomial has length at most $4$ , then it is cyclotomic.

We therefore restrict our attention to $P(z)\in \mathbb {Z}[z]$ satisfying:

(2.2) $$ \begin{align} & P(z)\textrm{ is monic;} \notag\\ & P(z)\textrm{ is reciprocal;} \notag\\ & P(z)\textrm{ is not cyclotomic;} \notag\\ & P(z)\textrm{ has length at least }5\,. \end{align} $$

To find the reciprocal shortness of a polynomial, one could adapt the algorithm in [9], although as the degree grows this is not especially attractive. (That algorithm works with the Euclidean norm of a polynomial rather than its length, but the authors comment that the algorithm could be adapted if length were the preferred measure. Also it does not restrict to reciprocal multiples, so potentially it could fail to deliver if a shorter non-reciprocal multiple exists.) If it turns out that the multiplier $T(z)$ is cyclotomic, than one has also found the cyclotomic shortness. The motivation in [9] was in finding a compact representation of an algebraic number.

If at least one of the zeros of $P(z)$ has modulus greater than $1$ (and this will be the only case of interest to us), then one can adapt an alternative method in [11, Section 1.7.1], and this was our chosen route.

Clearly reciprocal shortness is bounded above by cyclotomic shortness. There are examples where this inequality is strict. Consider the two polynomials

$$ \begin{align*} P_1(z) &= z^{45} - z^{42} + z^{36} - z^{34} - z^{32} + z^{31} - z^{24} + z^{21} - z^{14} + z^{13} + z^{11} - z^9 + z^3 - 1 \,\,, \\ P_2(z) &= z^{48} + z^{46} + z^{44} - z^{41} - z^{32} - z^{31} + z^{24} - z^{17} - z^{16} - z^7 + z^4 + z^2 + 1\,\,, \end{align*} $$

which appear on page 1703 of [13]. These are cyclotomic multiples of irreducible polynomials $Q_1(z)$ and $Q_2(z)$ of degrees $40$ and $44$ respectively: the shortest such cyclotomic multiples that Mossinghoff found. We adapted the algorithm in [11, Section 1.7.1] to seek only reciprocal multiples of a polynomial, and were able to check that in both cases these are indeed the shortest multiples of the noncylotomic parts by cyclotomic polynomials: the cyclotomic shortness of $Q_1(z)$ is $14$ , and the cyclotomic shortness of $Q_2(z)$ is $13$ . There are in fact $3$ reciprocal multiples of $Q_2(z)$ of length $13$ , and $21$ (!) reciprocal multiples of $Q_1(z)$ of length $14$ . The other two length- $13$ reciprocal multiples of $Q_2(x)$ are not cyclotomic multiples, but $Q_1(z)$ has an additional $5$ cyclotomic multiples that have length $14$ :

$$ \begin{align*} z^{47} + z^{46} - z^{42} - z^{41} + z^{37} - z^{33} - z^{30} + z^{17} + z^{14} - z^{10} + z^6 + z^5 - z - 1\,\,, \\ z^{58} - z^{55} - z^{53} + z^{49} - z^{41} + z^{40} + z^{31} - z^{27} - z^{18} + z^{17} - z^9 + z^5 + z^3 - 1\,\,, \\ z^{65} + z^{64} + z^{63} + z^{56} + z^{55} - z^{52} + z^{35} + z^{30} - z^{13} + z^{10} + z^9 + z^2 + z + 1\,\,, \\ z^{67} - z^{64} + z^{58} - z^{54} + z^{47} - z^{46} - z^{34} + z^{33} + z^{21} - z^{20} + z^{13} - z^9 + z^3 - 1\,\,, \\ z^{90} + z^{89} + z^{88} - z^{82} - z^{77} + z^{74} - z^{57} + z^{33} - z^{16} + z^{13} + z^8 - z^2 - z - 1\,\,. \end{align*} $$

For $Q_2$ , Mossinghoff noted a shorter reciprocal multiple that is not a cylotomic multiple:

$$\begin{align*}P_2'(z) = z^{56} + z^{51} - z^{50} + z^{47} - z^{39} - z^{28} - z^{17} + z^9 - z^6 + z^5 + 1\,. \end{align*}$$

He noted that one could, in principle, determine whether or not any other sparse multiples of $Q_1$ and $Q_2$ exist using the algorithm in [9]. Using our algorithm instead, we checked that $P_2'$ is the unique reciprocal multiple of $Q_2$ that has length below $13$ . Thus the cyclotomic shortness of $Q_2$ is $13$ and its reciprocal shortness is $11$ .

We also found a unique shorter reciprocal multiple of $Q_1$ , namely

$$\begin{align*}z^{101} + z^{97} - z^{90} - z^{88} - z^{74} + z^{63} + z^{38} - z^{27} - z^{13} - z^{11} + z^4 + 1\,. \end{align*}$$

This is not a cylotomic multiple of $Q_1$ , so that $Q_1$ too has cyclotomic shortness that is strictly larger than its reciprocal shortness ( $14>12$ ). These examples settle Problem 1.40 in [11].

We also verified that the polynomials listed in [11, Table D.1] are the shortest possible cyclotomic multiples of their non-cyclotomic factor, and we found all possible cyclotomic multiples of the same length.

Our first main result concerns shortness $5$ .

Theorem 2.2 Given $\varepsilon>0$ , there are only finitely many monic reciprocal polynomials $P(z)\in \mathbb {Z}[z]$ that have (reciprocal or cyclotomic) shortness $5$ and house at least $1+\varepsilon $ .

It will be enough to prove Theorem 2.2 for reciprocal shortness: if P has cyclotomic shortness $5$ then it is not cyclotomic (else it would divide $z^n-1$ for some n), and the reciprocal shortness must also be $5$ , after Remark 2.1 and the trivial inequality on the two flavours of shortness.

The analogous result for longer lengths is simply false. For even length $2\ell \ge 6$ , consider the polynomial $P_d(z) = (z-(\ell -1))z^d -(\ell - 1)z + 1$ , which is monic and reciprocal for all d. When d is large enough, $(z-(\ell -1))z^d$ dominates $(\ell -1)z-1$ on the circle $|z-(\ell -1)| = 0.5$ . By Rouchés Theorem, $P_d(z)$ has a zero within this circle for all sufficiently large d, and hence has house at least $\ell - 1.5$ . For odd length $2\ell +1\ge 7$ , one argues similarly with the polynomial $Q_d(z) = (z - (\ell -1))z^{2d-1} + z^d - (\ell -1)z + 1$ .

Given the focus on small Mahler measures (which is what restricted our attention to reciprocal polynomials anyway), it is pleasing that we can recover a finiteness result for length $6$ if we impose a suitable upper bound on the Mahler measure, and work with cyclotomic shortness.

Theorem 2.3 Let $\theta = 1.32471\cdots $ be the smallest Pisot number (the real root of the equation $z^3-z-1=0$ ). For any $\varepsilon>0$ and any $M<\theta $ , there are only finitely many monic reciprocal polynomials $P(z)\in \mathbb {Z}[z]$ that have cyclotomic shortness $6$ , house at least $1+\varepsilon $ , and Mahler measure at most M.

These finiteness results are effective: there are algorithms to produce all the finitely many polynomials claimed in Theorems 2.2 and 2.3.

A Salem number is a real algebraic integer $\tau $ greater than $1$ , degree at least $4$ , such that $1/\tau $ is a (Galois) conjugate of $\tau $ , and all other conjugates lie on the unit circle $|z|=1$ . A Salem number is equal to its house. As an immediate corollary of Theorems 2.2 and 2.3, along with algorithms for finding all the polynomials, we have the following.

Corollary 2.4 Let $\theta = 1.32471\cdots $ be the smallest Pisot number. For any interval $[a,b]$ with $1<a\le b<\theta $ , there is an algorithm to find all Salem numbers in that interval that have cyclotomic shortness at most $6$ .

We apply this to find all Salem numbers of cyclotomic shortness at most $6$ that lie in the interval $[1.17,1.3]$ .

Recall that if we seek monic reciprocal P with Mahler measure in the interval $(1,1.3)$ , then we may assume that the reciprocal shortness of $P(z)$ is at least $5$ . With this in mind, the plan for the rest of the paper is as follows. In the next two sections we treat shortness $5$ and shortness $6$ , including proofs of the two main theorems. In a final section we report some further computations, including the discovery of a new small Mahler measure with degree below $180$ .

3 Shortness 5, and the proof of Theorem 2.2

Now suppose that $P(z)$ has reciprocal shortness $5$ . Recall from (2.2) that $P(z)$ is a monic integer reciprocal polynomial that is not cyclotomic. Since $P(z)$ has reciprocal shortness $5$ , it divides a polynomial of the shape

(3.1) $$ \begin{align} z^n + \varepsilon_1 z^{n-g_1} + \varepsilon_2 z^{n-g_1-g_2} + \varepsilon_1 z^{g_1} + 1\,, \end{align} $$

where $n=2(g_1+g_2)$ , $g_1>0$ , $g_2 \ge 0$ , and $\varepsilon _1$ , $\varepsilon _2 \in \{1,-1\}$ . If $g_2=0$ , then we must have $\varepsilon _2 = \varepsilon _1$ , else our multiple of $P(z)$ would have length only $3$ .

Given $P(z)$ , one way to detect all such length- $5$ multiples is to loop over the possibilities for $\varepsilon _1$ and $\varepsilon _2$ , and for each choice obtain bounds for $g_1$ and $g_2$ (and hence, as it turns out, for n), as follows. Here we follow the algorithm in Section 1.7.1 of [11], noting how much simpler it is in this reciprocal case. We take a zero $\alpha $ of $P(z)$ for which $|\alpha |$ is maximal, and certainly we then have $|\alpha |>1$ , as P is not cyclotomic. Then . We note that if $g_1 \ge \log 4/\log |\alpha |$ , then

$$\begin{align*}|\alpha|^n \ge 4|\alpha|^{n-g_1}> |\varepsilon_1 \alpha^{n-g_1} + \varepsilon_2\alpha^{n-g_1-g_2} + \varepsilon_1\alpha^{g_1} + 1 |\,, \end{align*}$$

contradicting $P(\alpha )=0$ (as then (3.1) would also vanish). Thus

(3.2) $$ \begin{align} 0< g_1 \le \lfloor \log 4/\log|\alpha| \rfloor\,. \end{align} $$

Then we have

$$\begin{align*}|\varepsilon_2 \alpha^{n-g_1-g_2} + \varepsilon_1 \alpha^{g_1} + 1 | < 3|\alpha|^{n-g_1-g_2} \end{align*}$$

and

$$\begin{align*}|\alpha|^{n-g_1}\Big||\alpha|^{g_1} - 1\Big| \le |\alpha^{n}+ \varepsilon_1\alpha^{n-g_1}|\,, \end{align*}$$

so if $g_2 \ge (\log 3 - \log (|\alpha |^{g_1}-1))/\log |\alpha |$ , then (3.1) cannot vanish. We conclude that

(3.3) $$ \begin{align} 0\le g_2 \le \lfloor (\log 3 - \log(|\alpha|^{g_1}-1))/\log|\alpha|\rfloor\,. \end{align} $$

In fact, given specific $\varepsilon _1$ and $\alpha $ , one should use the more precise upper bound

$$\begin{align*}g_2 \le \lfloor (\log 3 - \log|\alpha^{g_1} + \varepsilon_1|))/\log|\alpha| \rfloor \,, \end{align*}$$

but for the proof of Theorem 2.2 we use that the bound in (3.3) depends only on . We see from (3.2) and (3.3) that $g_1$ and $g_2$ are bounded once $P(z)$ is given, but moreover we can bound $g_1$ and $g_2$ merely given a lower bound for the house of $\alpha $ . Just to stress this point: we started with a particular $P(z)$ in mind, but then noticed that the finite list of possible multiples can be generated knowing only a lower bound for the house.

This establishes Theorem 2.2, and indeed we have an algorithm to find all the monic reciprocal polynomials that have length $5$ and house above a given bound.

For example, let us find all monic reciprocal length- $5$ polynomials that have house at least Lehmer’s number. The bounds (3.2) and (3.3) give $0<g_1\le 8$ , and $0\le g_2 \le 17$ (in the worst case: it is better to use (3.3) with the current value of $g_1$ ). A quick search, checking which of these polynomials actually have house at least Lehmer’s number yields Table 1. We only include one of the polynomials $P(z)$ , $P(-z)$ , as these trivially have the same house and Mahler measure, and noting that $P(z^d)$ also has the same Mahler measure as $P(z)$ , we restrict to ‘primitive’ polynomials in the output (those that cannot be written as $P(z^d)$ for any $d>1$ ). The house of $P(z^d)$ is the dth root of the house of $P(z)$ , so only finitely many imprimitive polynomials would appear if we included them. Where more than one cyclotomic multiple of the minimal polynomial has length 5, the different multiples are grouped together without repeating the house and measure.

Table 1 All primitive monic reciprocal polynomials in $\mathbb {Z}[z]$ that have length $5$ and house at least Lehmer’s number, along with their Mahler measures. Only one of $P(z)$ and $P(-z)$ is shown.

All but one of the examples in Table 1 is actually a Salem number: the house equals the Mahler measure. In each case the reciprocal multiple turned out to be a cyclotomic multiple. Note that up to changing the sign of z, the table shows all length- $5$ primitive polynomials that have that house. For example, the only primitive length- $5$ monic reciprocal polynomials that have Mahler measure equal to Lehmer’s number are the two shown in this table along with the two obtained by changing the sign of z. (If one does not require reciprocal multiples, there are four other length- $5$ multiples of Lehmer’s polynomial: $z^{19} - z^{18} - z^6 - z^3 + 1$ , $z^{15} - z^{13} - z^5 - z^4 + 1$ , $z^{19} - z^{16} - z^{13} - z + 1$ , and $z^{15} - z^{11} - z^{10} - z^2 + 1$ . These were found using the algorithm in Section 1.7.1 of [11].)

One byproduct of the above short computation is that the largest house for any length- $5$ monic reciprocal polynomial is for the polynomial $z^2 \pm 3z + 1$ , with house $2.618\cdots $ .

There are many thousands of small Mahler measures that are represented by length $5$ polynomials, although not many tiny ones are known. To find all of these, one needs to push the house bound closer to $1$ .

We tried reducing the house bound, and counting the numbers of small and tiny measures found. For the small measures, we restricted the output to the cases where the minimal polynomial had degree at most $180$ , for comparison with Mossinghoff’s data, but with no restriction on the degree of the short multiple. For the tiny measures, no upper bound on the degree was imposed, but in fact the degrees were all relatively small: the largest was $32$ , for the polynomial $z^{32} + z^{31} + z^{16} + z + 1$ . We found that there are $4994$ length- $5$ polynomials that have Mahler measure in the interval $(1,1.3)$ , degree at most $180$ , and house at least $1.01$ . These cover more than half of the known small Mahler measures that have degree below $180$ . The smallest house found in this search was $1.010397\cdots $ , for the polynomial $z^{186} + z^{94} + z^{93} + z^{92} + 1$ (a cyclotomic multiple of a degree- $180$ non-cyclotomic polynomial that has Mahler measure $1.2837785\cdots $ ). All $15$ of the known tiny Mahler measures that have shortness $5$ were found, and this list is now known to be complete for house at least $1.01$ . The smallest house amongst these is $1.08376\cdots $ (rather larger than the bound of $1.01$ for which the list is now known to be complete), for the polynomial $z^{24}+z^{13}-z^{12}+z^{11}+1$ . All computations were performed using the PARI-gp package [1], running on a 3GHz processor. The data for Table 1 was computed in a fraction of a second. Pushing the lower bound on the house down to $1.01$ took $13$ hours.

4 Shortness 6, and the proof of Theorem 2.3

Now suppose that $P(z)$ (monic, reciprocal, not cyclotomic, as in (2.2)) has cyclotomic shortness $6$ . Then $P(z)$ divides a polynomial of the shape

$$\begin{align*}Q(z)z^k + \eta Q^*(z)\,, \end{align*}$$

where $Q^*(z) = z^{\mathrm {deg}(Q)} Q(1/z)$ , $\eta \in \{-1,1\}$ , and

$$\begin{align*}Q(z) = z^{g_1+g_2} + \varepsilon_1 z^{g_2} + \varepsilon_2 \end{align*}$$

for some $\varepsilon _1$ , $\varepsilon _2 \in \{-1,1\}$ , $g_1>0$ , $g_2\ge 0$ , with $\varepsilon _1=\varepsilon _2$ if $g_2=0$ . We have $k\ge \mathrm {deg}(Q)$ , and if $k = \mathrm {deg}(Q)$ then $\eta = 1$ . We note also that $Q(z)$ is not reciprocal, else (Remark 2.1) it would be cyclotomic, and then $P(z) = Q(z)(z^k\pm 1)$ would also be cyclotomic.

We impose an upper bound M on the Mahler measure of $P(z)$ that is lower than $\theta = 1.32\cdots $ , so is lower than the Mahler measure of $Q(z)$ , as Q is not reciprocal (using Smyth’s theorem [17]):

(4.1) $$ \begin{align} M(P)\le M<\theta \le M(Q)\,. \end{align} $$

If , then arguing as in the previous section one computes

(4.2) $$ \begin{align} 0 < g_1 \le \lfloor \log 5/ \log(1 + \varepsilon) \rfloor \end{align} $$

and

(4.3) $$ \begin{align} 0\le g_2 \le \lfloor (\log 4 - \log((1+\varepsilon)^{g_1} - 1))/\log(1+\varepsilon) \rfloor\,. \end{align} $$

There is, however, no upper bound on the next gap in the degree sequence of P (so no upper bound on k) that depends only on a lower bound for the house, as our examples between the statements of Theorems 2.2 and 2.3 show.

On the other hand, as $k\to \infty $ , a Rouché argument (adapting Salem’s argument, as simplified by Hirschman, [16, p. 30]) shows that the Mahler measure of $Q(z)z^k + \eta Q^*(z)$ tends to the Mahler measure of $Q(z)$ . We give the full detail, in preparation for making it algorithmically effective. For any real $\gamma>0$ , and any positive integer k, define

$$\begin{align*}R_{\gamma,k}(z) = (1+\gamma)Q(z)z^k + \eta Q^*(z)\,. \end{align*}$$

If $|\alpha |=1$ and $Q(\alpha )=0$ , then also $0 = Q(\overline {\alpha }) = Q(1/\alpha )$ , whence $Q^*(\alpha )=0$ . Putting $T(z) = \prod _{|\alpha |=1, Q(\alpha )=0}(z-\alpha )$ (counting with multiplicity, but see Lemma 4.1), we have that $R_{\gamma ,k}(z)/T(z)$ is a polynomial (with real coefficients). Moreover, on $|z|=1$ we have $|Q(z)|=|Q^*(z)|$ , and hence $|(1+\gamma )Q(z)z^k/T(z)|> |\eta Q^*(z)/T(z)|$ . Suppose that $Q(z)$ has degree m and has t zeros outside the unit disc, and $u=\deg (T)$ zeros on the unit circle. Applying Rouché’s Theorem with the contour $|z|=1$ , we conclude that $R_{\gamma ,k}/T(z)$ has exactly $m-t-u+k$ zeros in the open unit disc, and hence that $R_{\gamma ,k}$ has exactly $m-t+k$ zeros in the closed unit disc. Letting $\gamma \to 0$ these zeros vary continuously in the complex plane, and hence, for any positive integer k, $Q(z)z^k + \eta Q^*(z)$ has at least $m-t+k$ zeros in the closed unit disc.

Now take $\delta>0$ small enough that circles of radius $\delta $ centered on the t zeros of Q outside the unit disc do not overlap, and do not touch the unit circle. On each such circle, when k is large enough, $|Q(z)z^k|>|\eta Q^*(z)|$ , and hence by Rouché’s Theorem there is a single zero of $Q(z)z^k + \eta Q^*(z)$ inside the circle. Hence, for k large enough, the Mahler measure of $Q(z)z^k + \eta Q^*(z)$ lies between $\prod _{|\alpha |>1,Q(\alpha )=0} (|\alpha |-\delta )$ and $\prod _{|\alpha |>1,Q(\alpha )=0} (|\alpha |+\delta )$ . Letting $\delta \to 0$ , we see that as $k\to \infty $ the Mahler measure of $Q(z)z^k + \eta Q^*(z)$ tends to the Mahler measure of $Q(z)$ .

Given (4.1), we see that for all $k\ge k_0$ (where $k_0$ depends on Q) no cyclotomic multiple of P can equal $Q(z)z^k + \eta Q^*(z)$ . We have established Theorem 2.3: given $\varepsilon>0$ we get finitely many possibilities for Q as above such that $Q(z)z^k + \eta Q^*(z)$ can possibly have house $\ge 1 + \varepsilon $ ; for each such Q we get finitely many k for which $Q(z)z^k + \eta Q^*(z)$ can possibly be a multiple of $P(z)$ by a cyclotomic polynomial (given our upper bound on the Mahler measure of P; here restricting to cyclotomic multiples so as to preserve the Mahler measure).

To make this finiteness result algorithmically effective, we need to perform explicit Rouché estimates. Although one can cope with the zeros of $Q(z)$ not all being simple, we make the remark that for our special $Q(z)$ there can be no multiple zeros.

Lemma 4.1 Let $Q(z) = z^{a} + \varepsilon _1 z^b + \varepsilon _2$ , where $a>b\ge 0$ , and $\varepsilon _1$ , $\varepsilon _2\in \{-1,1\}$ , with $\varepsilon _1=\varepsilon _2$ if $b=0$ . Then $Q(z)$ has no multiple zeros.

Proof Since $z^a \pm 2$ has only simple zeros, we can immediately move to the case $a>b>0$ . Any zero of $Q(z)$ that is not simple would also be a zero of $Q'(z) = az^{a-1} + b\varepsilon _1 z^{b-1}$ . This gives $|z|^{a-b}=b/a$ . On the other hand, eliminating the leading terms of $Q(z)$ and $Q'(z)$ gives $(a-b)\varepsilon _1 z^b + a\varepsilon _2 = 0$ , so that $|z|^b = a/(a-b)$ . Hence $|z|^{(a-b)b} = b^b/a^b = a^{a-b}/(a-b)^{a-b}$ , which gives $b^b(a-b)^{a-b} = a^ba^{a-b}$ , contradicting $0<b<a$ .

Now we suppose that $P(z)$ has Mahler measure at most M, with M less than the Mahler measure of Q. Label the zeros of Q as $\alpha _1$ , …, $\alpha _p$ , where $|\alpha _1| \ge \cdots \ge |\alpha _q|> 1 \ge |\alpha _{q+1}| \ge \cdots \ge |\alpha _p|$ (so that the Mahler measure of Q is $|\alpha _1\cdots \alpha _q|$ ). For a radius $\delta>0$ , we shall call the circle $|z-\alpha _i|=\delta $ good if it does not meet the unit circle $|z|=1$ .

We choose $\delta $ small enough and $k_0$ large enough so that

1. (i) the circles $|z-\alpha _i| = \delta $ , for $1\le i\le q$ do not intersect;

2. (ii) the product of the $|\alpha _i|-\delta $ over good circles (still with $1\le i\le q$ ) is at least M;

3. (iii) $|z^kQ(z)|$ dominates $|Q^*(z)|$ on each of these good circles, for all $k> k_0$ .

We shall turn in a moment to how we deal with (iii). Taking $\delta $ small enough one could make all the circles $|z-\alpha _i| = \delta $ good, for $1\le i\le q$ . In practice, however, one or more of the $\alpha _i$ outside the unit circle might have modulus very close to $1$ , and one may get a better value of $k_0$ by working only with zeros of larger modulus, allowing $\delta $ to be a little larger. Once we have our $\delta $ and $k_0$ , Rouché’s Theorem tells us that $Q(z)z^k + \eta Q^*(z)$ has a (single, simple) zero inside each good circle for all $k> k_0$ , and hence (using (ii)) that the Mahler measure of $Q(z)z^k + \eta Q^*(z)$ is larger than M for all $k\ge k_0$ . This tells us that for this $Q(z)$ we can bound k above by $k_0$ .

In order to apply this approach, we need to obtain a lower bound for $|Q(z)|$ on each good circle, and an upper bound for $|Q^*(z)|$ . Here our tactics diverge, according to whether we want to have a provable bound, where we are sure that our bound on k is large enough, or whether we would rather use a stronger bound that is highly likely to be correct, but that relies on numerical estimates that come with no guarantee of sufficient accuracy. The latter, rough, approach is simplest: we take a large sample of points on each circle to estimate the minimum of $|Q(z)/Q^*(z)|$ on the circle (assuming $\delta $ small enough that $Q^*$ has no zeros in or on the circle), and hence obtain an unproven bound for k that will likely be large enough. To obtain provable bounds for k, on the other hand, we expand $Q(z)$ about each $\alpha _i$ , obtaining the coefficients to high accuracy, and then take $\delta $ small enough that the multiple of $|z-\alpha _i|$ dominates all the other terms when z is on the circle; and for the same $\delta $ we then obtain an upper bound for $|Q^*(z)|$ on the same circle, simply using the triangle inequality. This approach gives weaker but provable bounds for k, for each $Q(z)$ .

A partial example will help to clarify this computation of provable bounds, and will indicate some other features of the way that the provable computation was organised. Suppose we are seeking house at least $1.1$ , which is comfortably greater than $1$ , and tiny Mahler measure (at most $1.25$ , which is comfortably below $\theta $ ). Write $Q(z) = z^{g_1+g_2} + \varepsilon _1z^{g_2} + \varepsilon _2$ , so that $g_1$ and $g_2$ are our first two gaps in the degree sequence of Q (or P). Then (4.2) and (4.3) give

$$\begin{align*}1\le g_1 \le \lfloor \log 5/\log 1.1 \rfloor = 16\,, \end{align*}$$

and

$$\begin{align*}0\le g_2 \le \lfloor (\log 4 - \log( 1.1^4 - 1) )/\log1.1 \rfloor = 22\,. \end{align*}$$

We loop over these. Let us focus on what happens when $g_1=4$ and $g_2 = 2$ . We now loop over the possible signs $\varepsilon _1$ and $\varepsilon _2$ : let us consider when they both equal $-1$ . So we are looking at $Q(z) = z^6 - z^2 - 1$ , with $Q^*(z) = -z^6 - z^4 + 1$ .

Our aimed-for polynomial $P(z)$ has the shape $P(z) = Q(z)z^k \pm Q^*(z)$ , but we make here two observations that we used in practice to cut down the number of polynomials considered. First, if k were even then $P(z)$ would not be primitive: it would have the same Mahler measure as $(z^3 - z - 1)z^{k/2}\pm (-z^3-z^2+1)$ , which would have been considered already with smaller values for the gaps. In general, we restrict to $\gcd (g_1,g_2,k)=1$ . Next, since k is odd in this case, we need only consider $P(z) = Q(z)z^k + z^6+z^4 - 1$ , as changing the sign of z gives a polynomial with the same Mahler measure. In general, we halve the number of polyomials to be considered by insisting that after the first odd gap in the list of $6$ exponents for the powers of z appearing in $P(z)$ , the coefficient should be positive (and we cannot have all gaps even, or the polynomial would not be primitive).

We know that as $k\to \infty $ , the Mahler measure of $(z^6-z^2-1)z^k + z^6+z^4-1$ approaches the Mahler measure of $z^6-z^2-1$ , which is $1.3247\cdots $ , so for large enough k the Mahler measure will not be tiny. We use an explicit Rouché estimate to bound k.

The zeros of $Q(z)$ outside the unit circle are $\pm \alpha $ , where $\alpha = 1.15096\cdots $ . If we take $\delta =0.03$ , then if k is large enough that $P(z)$ has a zero inside both of the circles ${|z-(\pm \alpha )|=\delta} $ , then the Mahler measure of P will be at least $(|\alpha |-\delta )^2 = 1.2565\cdots $ , and so the measure will not be tiny. See Figure 1.

Figure 1 A diagram showing the six zeros of $Q(z)$ (marked as $\cdot $ ), and circles of radius $\delta $ around the two zeros outside the unit circle; there is room to draw larger circles around these zeros and still miss the unit circle, but we must take them small enough that if $Q(z)z^k+\eta Q^*(z)$ has a zero in each of these small circles then its Mahler measure is greater than $1.25$ .

We want k large enough that $(z^6-z^2-1)z^k$ dominates $z^6+z^4-1$ on both circles. We could get an upper bound for $|z^6 + z^4 - 1|$ simply by using the triangle inequality, but we get a slightly better bound if we expand $z^6+z^4-1$ about each of the centres of the circles, and then use the triangle inequality: we find $|z^6+z^4-1|\le 3.66$ on both circles.

Expanding $Q(z)$ about $z=\alpha $ , we get $Q(z) = (9.817\cdots )(z-\alpha ) + (25.32\cdots )(z-\alpha )^2 + \cdots + (z - \alpha )^6$ . Our chosen radius $\delta $ is such that $(9.817\cdots )\delta $ dominates $(25.32\cdots )\delta ^2 + \cdots + \delta ^6$ , and so we can use the triangle inequality to get a lower bound of $(9.817\cdots )\delta - (25.32 \cdots )\delta ^2 - \cdots - \delta ^6$ for $|Q(z)|$ on this circle. This gives a lower bound of $0.27$ . Note that if our lower bound here were negative, we would simply decrease $\delta $ appropriately.

Now for $k\ge 23$ , we have $0.27(\alpha -0.03)^k>3.66$ . We conclude that if $k\ge 23$ then $z^kQ(z)$ dominates $Q^*(z)$ on each of our good circles, and the Mahler measure of P will not then be tiny. Thus we loop over $k=1$ , $3$ , $5$ , …, $21$ to complete this choice of $Q(z)$ . The results of this computation are shown in Table 2.

Table 2 A part of the output of computations to find all length- $6$ polynomials that have house at least $1.1$ and Mahler measure below $1.25$ .

We see from Table 2 that there are four tiny Mahler measures coming from this choice of $Q(z)$ , corresponding to $k=7$ , $9$ , $11$ , $13$ , ignoring any that would have been picked up with $Q(z) = z^3 - z - 1$ .

We used the algorithm described above to find all primitive monic integer polynomials that have length $6$ , house at least Lehmer’s number ( $1.17\cdots $ ), and measure at most $1.3$ . As the number of polynomials is rather large, we limit the presentation of our output to: (i) (Table 3) a list of all such polynomials (up to change of sign of the variable) that have tiny measure (below $1.25$ ) — these were all Salem numbers (so their house equals their Mahler measure); and (ii) (Table 4) a list of all small measures found, indicating which are Salem numbers, without listing all the polynomials.

Of the measures in Table 4, all but $4$ are Salem numbers. There are a further $11$ Salem numbers known in the interval $(1.17,1.3)$ , and for completeness we list them here, along with their cyclotomic shortness.

The polynomials in Table 5 are the minimal-degree examples for that minimal length. The complete list of polynomials is finite, and includes some remarkable examples, such as $z^{144} + z^{143} - z^{140} + z^{136} - z^{113} - z^{108} - z^{36} - z^{31} + z^8 - z^4 + z + 1$ , which has a degree- $110$ cyclotomic factor. The cyclotomic shortnesses were computed using the algorithm in Section 1.7.1 of [11], adapted to finding reciprocal multiples; in all cases here the reciprocal multiplier turned out to be cyclotomic, so that the (cyclotomic) shortness had indeed been determined.

Table 3 All primitive monic polynomials in $\mathbb {Z}[z]$ that have length $6$ , house at least Lehmer’s number, and Mahler measure at most $1.25$ . Only one of $P(z)$ and $\pm P(-z)$ is shown. All are Salem numbers.

Table 4 All Mahler measures in the interval $(1.17,1.3)$ that have house at least Lehmer’s number and shortness at most $6$ (as it happens, all are covered by length- $6$ polynomials), along with a minimal-degree length $6$ polynomial for each measure. Measures that are not Salem numbers are shown in bold.

Table 5 Small Salem numbers that have cyclotomic shortness s greater than $6$ ; the degree d of the Salem number is also shown.

To catch more measures, we pushed the house bound lower, to $1.01$ , but to make the computations manageable we also imposed a limit of $512$ on the degree of the short polynomial (rather larger than in previous searches), and with a bound of $180$ on the degree of the noncyclotomic part (for comparison with existing tables). With these parameters, the largest degree seen for a primitive polynomial was $370$ (polynomial $x^{370} + x^{368} + x^{277} - x^{93} - x^2 - 1$ , house $1.03023\cdots $ , measure $1.28697\cdots $ , cyclotomic factor of degree $190$ ) so that it is plausible that this search too has found all examples regardless of the degree, for the given house and measure parameters, and with a bound on the degree of the noncyclotomic part. We found $8002$ small length- $6$ measures, including all the shortness- $5$ measures as a subset, and including all the known tiny length- $6$ examples. The smallest house found was the same as in the length- $5$ search ( $1.010397$ ), but now we found a length- $6$ multiple of the minimal polynomial: $x^{187} + x^{186} + x^{95} + x^{92} + x + 1$ . The computations for Tables 3 and 4 took less than a minute. Pushing the lower bound on the house down to $1.01$ , with the restrictions mentioned above, took $62$ hours.

5 Opportunistic searches and a new small measure

For length- $7$ reciprocal polynomials, the general shape is $P(z) = Q(z)z^k \pm z^\ell + Q^*(z)$ , where $Q(z)$ has length $3$ . Unlike the length- $6$ case, we can have Q reciprocal (and hence cyclotomic). But just as for lengths $5$ and $6$ , if we have a lower bound greater than $1$ for the house, then the first two gaps in the degree sequence of our polynomial are bounded, and we get finitely many possibilities for $Q(z)$ . As the third gap $k-\ell \to \infty $ , the Mahler measure of P approaches at least that of Q (another Rouché argument; unless Q is cyclotomic, when this estimate is trivial). This suggests a way of cutting down on the possibilities for length $7$ (and similar ideas permeate to longer polynomials): we only push our search hard if the Mahler measure of Q is small.

For example, with length $7$ we tried a house bound of $1.02$ , and a bound of $1.4$ for the Mahler measure of Q. With these parameters, our search found many known small Mahler measures, and one new one:

$$\begin{align*}z^{186} - z^{157} - z^{154} + z^{93} - z^{32} - z^{29} + 1 \end{align*}$$

is a cyclotomic multiple of the irreducible polynomial

$$ \begin{align*} z^{178} &+ z^{177} + z^{176} - z^{173} - z^{172} - z^{171} + z^{163} + z^{162} + z^{161} - z^{158} - z^{157} - z^{156} - z^{149} - z^{145} \\& + z^{140} + z^{139} - z^{134} - z^{130} + z^{125} + z^{124} - z^{119} - z^{115} + z^{110} + z^{109} - z^{104} - z^{100} + z^{95} \\ &+ z^{94} - z^{89} + z^{84} + z^{83} - z^{78} - z^{74} + z^{69} + z^{68} - z^{63} - z^{59} + z^{54} + z^{53} - z^{48} - z^{44} \\ &+ z^{39}+ z^{38} - z^{33} - z^{29} - z^{22} - z^{21} - z^{20} + z^{17} + z^{16} + z^{15} - z^7 - z^6 - z^5 + z^2 + z + 1, \end{align*} $$

which has degree $178$ , house $1.02007$ , and Mahler measure $1.2948243\cdots $ . This does not appear on any of the existing lists. It was the only new example that we found.