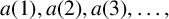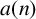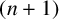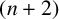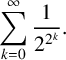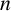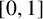3 results
THE SUMMED PAPERFOLDING SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 189-198
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
BINARY SIGNED-DIGIT REPRESENTATIONS IN PAPERFOLDING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 363-375
- Print publication:
- December 2022
-
- Article
- Export citation
POINTS IN A FOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 7-17
- Print publication:
- August 2022
-
- Article
- Export citation