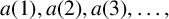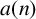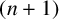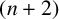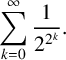THE SUMMED PAPERFOLDING SEQUENCE

Abstract

The sequence $a( 1) ,a( 2) ,a( 3) ,\ldots, $ labelled A088431 in the Online Encyclopedia of Integer Sequences, is defined by: $a( n) $ is half of the $( n+1) $th component, that is, the $( n+2) $th term, of the continued fraction expansion of

$$ \begin{align*} \sum_{k=0}^{\infty }\frac{1}{2^{2^{k}}}. \end{align*} $$

Dimitri Hendriks has suggested that it is the sequence of run lengths of the paperfolding sequence, A014577. This paper proves several results for this summed paperfolding sequence and confirms Hendriks’s conjecture.

1. Introduction and preliminaries

According to Ben-Abraham et al. [4], the regular paperfolding sequence was discovered in the mid-1960s by three NASA physicists: John Heighway, Bruce Banks and William Hartner. Martin Gardner celebrated their work in Scientific American [7], after which Davis and Knuth [5] developed the mathematical underpinnings of paperfolding. Since that time, many papers have been written exploring the diverse features of this sequence, notably Dekking et al. [6], Allouche and Shallit [1], Mendès France and van der Poorten [9], and Mendès France and Shallit [8].

We start with two alternative definitions of sequence A088431, both found in the Online Encyclopedia of Integer Sequences [13].

Definition 1.1 (A088431 continued fraction definition [13]).

The sequence $ {A=a( 1) a( 2) a( 3) \ldots }$ is defined by: $a( n) $ is half of the $ ( n+1) $ th component, that is, the $( n+2) $ th term, of the continued fraction expansion of

$$ \begin{align*} \sum_{k=0}^{\infty }\frac{1}{2^{2^{k}}}. \end{align*} $$

Definition 1.2 (A088431 alternative definition [13]).

The sequence ${A=a( 1) a( 2) a( 3) \ldots } $ is given by the following rule: let $ i=1,2,3,\ldots $ and $a( 1) =2.$ Then

$$ \begin{align*} a( a( 1) +a( 2) +a( 3) +\cdots +a( n) +1) =2 \end{align*} $$

and the ith undefined term of A is the ith term of the sequence

$$ \begin{align*} 1,3,1,3,1,3,1,3,1,3,1,3,\ldots. \end{align*} $$

Example 1.3. Based on Definition 1.2, we give the first few terms of the sequence A088431 in Table 1.

Table 1 Initial terms of the sequence A088431.

Dimitri Hendriks in [13] has suggested that sequence A088431 appears to be the sequence of run lengths of the regular paperfolding sequence A014577. We prove several results concerning this summed paperfolding sequence and confirm Hendriks’s conjecture.

In what follows, for simplicity and where no ambiguity exists, we remove the commas from sequences. For example, for a sequence only having values $1,2$ or $3,$ the sequence $2,2,1,3$ becomes $2213.$

Davis and Knuth [5] prove the following result which we adopt as a definition for the paperfolding sequence. The notation is taken from Bates et al. [2].

Definition 1.4 (Paperfolding sequence).

Let $S_{n}$ be the paperfolding sequence of length $2^{n}-1$ and let $\overline {\text { }S_{n}^{R}}$ be $S_{n}$ in reverse order with $0$ becoming $1$ and $1$ becoming $0$ . Then, $ S_{1}=1,\label {zd} S_{n+1} =S_{n}1\overline {S_{n}^{R}}$ and $\overline {S_{n+1}^{R}} =S_{n}0\overline {\text { }S_{n}^{R}}$ .

Bates et al. [2, 3] identify the following results for $ S_{n}$ .

Theorem 1.5 (Expression for $S_{n}$ ).

For $n>0$ and $h,k\geq 0$ , $ S_{n}=f_{1}f_{2}\ldots f_{2^{n}-1}$ , where

$$ \begin{align*} f_{i}=\left\{ \begin{array}{@{}ll} 1 &\text{if }i=2^{k}(4h+1), \\ 0 &\text{if }i=2^{k}(4h+3). \end{array} \right. \end{align*} $$

Theorem 1.6 (Paperfolding runs).

The paperfolding sequence, $S_{n}$ , contains only runs of single, double or triple entries of $0;$ or single, double or triple entries of $1.$ In particular, for $n\geq 4,\ S_{n}$ contains:

1. (i) $2^{n-4}$ instances of the triple $111,$ and $2^{n-4}-1$ instances of the triple $000;$

2. (ii) $2^{n-3}$ instances of the double $11,$ and $2^{n-3}+1$ instances of the double $00;$

3. (iii) $2^{n-4}$ instances each of the single $1,$ and the single $0.$

Theorem 1.7 (Interleaved paperfolding).

Let $S=f_{1}f_{2}f_{3}\ldots $ be the paperfolding sequence of infinite length. Then

$$ \begin{align*} S=S_{3}\text{ }f_{1}\overline{\text{ }S_{3}^{R}}\text{ }f_{2}\text{ }S_{3} \text{ }f_{3}\overline{\text{ }S_{3}^{R}}\text{ }f_{4}\text{ }S_{3}\text{ } f_{5}\overline{\text{ }S_{3}^{R}}\text{ }\ldots. \end{align*} $$

That is, S is formed from the alternating interleave of two subsequences, $ S_{3}$ and $\overline {\text { }S_{3}^{R}},$ with itself. $\label {o}$

We consider the runs of identical terms in $S_{n}$ or $S,$ that is, the sizes of the sequence of successive digits $1$ and $0$ of $S_{n}$ or $S.$ We begin with a definition of these runs.

Definition 1.8 (Summed paperfolding sequence).

For $S_{n}=f_{1}f_{2}\ldots f_{2^{n}-1}$ :

• • the summed paperfolding sequence, $G_{n}$ , is the sequence of the sizes of successive digits $1$ and $0$ of $S_{n};$

• • the summed paperfolding sequence of infinite length is $ G=\lim _{n\rightarrow \infty }\ G_{n}$ and is designated as $G=g( 1) g( 2) g( 3) \ldots $

We show in Theorem 1.10 that $G_{n}$ has length $2^{n-1}.$

Example 1.9. $S_{4} =110110011100100, G_{4} =21223212$ and $G =21223212\ldots .$

The key results in this paper are:

• • Theorem 2.1, a closed-form expression for G analogous to the expression for $S_{n}$ (and by extension $S)$ given at Theorem 1.5;

• • Theorem 2.2 identifying the main internal relationships within G;

• • Theorem 4.1 (Main Result) confirming Hendriks’s conjecture [13]. That is, the sequence $A=a( 1) a( 2) a( 3) \ldots $ of A088431 is exactly the sequence ${G=g( 1) g( 2) g( 3) \ldots } $ of Definition 1.8.

Theorem 1.10 (Length of $G_{n}$ ).

$\vert G_{n}\vert =2^{n-1}, $ where $\vert G_{n}\vert $ is the length of $G_{n}. \label {ze}$

Proof. For $n<4$ , our result is true. From Theorem 1.6, for $n\geq 4,$ there are $2^{n-4}\ 111\mathrm{s}$ , $2^{n-4}-1\ 000\mathrm{s}$ , $2^{n-3}\ 11\mathrm{s}$ , $2^{n-3}+1\ 00\mathrm{s}$ , $2^{n-4}\ 1\mathrm{s}$ and $2^{n-4}\ 0\mathrm{s}$ . Hence,

$$ \begin{align*} \vert G_{n}\vert =2^{n-4}+2^{n-4}-1+2^{n-3}+2^{n-3}+1+2^{n-4}+2^{n-4} =2^{n-1}.\\[-34pt] \end{align*} $$

Note that from Definition 1.4, since $S_{n+1}=S_{n}1\overline {S_{n}^{R}} ,$ the initial $\vert G_{n}\vert $ terms of $G_{n+1}$ will be $ G_{n}.$ Since by Theorem 1.10, $\vert G_{n}\vert =2^{n-1}$ , we can write

$$ \begin{align*} G_{n}=g( 1) g( 2) \ldots g( 2^{n-1}-1) g( 2^{n-1}) \text{.} \end{align*} $$

2. Basic facts concerning G

We now develop an analogous expression for G to that given at Theorem 1.5 for $S_{n}$ (and, by extension, S).

Theorem 2.1 (Expression for G).

For $h,k,p\geq 0$ , $G=g( 1) g( 2) g( 3) \ldots ,$ where

$$ \begin{align*} g( n) = \begin{cases} 1\text{ if (i) }n=8k+2\text{, or } \\\quad\ \text{if (ii) }n=8k+7, \\2\text{ if (iii) }n=8k+1\text{ and }k=2^{p}( 4h+3),\text{ or} \\\quad\ \text{if (iv) }n=8k+3,\text{ or} \\\quad\ \text{if (v) }n=8k+4\text{ and }k\text{ is even},\text{ or} \\\quad\ \text{if (vi) }n=8k+5\text{ and }k\text{ is odd, or} \\\quad\ \text{if (vii) }n=8k+6\text{, or} \\\quad\ \text{if (viii) }n=8k+8\text{ and }k+1=2^{p}( 4h+1). \\3\text{ if (ix) }n=8k+1\text{ and }k=2^{p}( 4h+1) ,\text{ or} \\\quad\ \text{if (x) }n=8k+4\text{ and }k\text{ is odd, or} \\\quad\ \text{if (xi) }n=8k+5\text{ and }k\text{ is even, or} \\\quad\ \text{if (xii) }n=8k+8\text{ and }k+1=2^{p}( 4h+3) \text{.} \end{cases} \end{align*} $$

Proof. From Theorem 1.6, S only contains singles, doubles and triples. Thus, the only possible terms in G are $1,\ 2$ and $3.$ From Theorem 1.7, each $S_{3}$ and $\overline {\text { }S_{3}^{R}}$ starts with $11$ and ends with $00$ and the component $S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$ is followed by $S_{3}\ f_{i+2}\overline {\text { }S_{3}^{R}}\ f_{i+3},$ which is followed by $S_{3}\ f_{i+4}\overline {\text { }S_{3}^{R}}\ f_{i+5},$ and so on, indefinitely. Let the $0$ th component be $S_{3}\ f_{1} \overline {\text { }S_{3}^{R}}\ f_{2}.$ Then the kth component is $S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$ where i is odd and ${k={(i-1)}/{2}}$ . Thus, the translation from S to G of the kth component, $ S_{3} \ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1},$ can be represented by eight terms, $g( 8k+1) $ to $g( 8k+8) ,$ where $k={(i-1)}/{2}$ with two possible configurations:

• • $f_{i}=0:\ S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$ becomes ( $2$ or $3)123221(2$ or $3);$ or

• • $f_{i}=1:\ S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$ becomes ( $2$ or $3)122321(2$ or $3)$ ,

where bracketed entries are determined by the values of $f_{i-1}$ and $ f_{i+1}.$

We consider each of $g( n) =1,\ 3$ and $2$ separately.

1. (1) $g( n) =1.$ In the $8$ -term translations above, we have $ g( 8k+2) $ and $g( 8k+7) $ always taking the value $1,$ irrespective of the values of $f_{i-1},f_{i}$ or $f_{i+1},$ and there are no other values of $1$ in this $8$ -term translation. Thus, $g( n) =1$ if $n=8k+2$ or $8k+7.$

2. (2) $g( n) =3.$ Consider the component $S_{3}\ f_{i}\overline { \text { }S_{3}^{R}}\ f_{i+1}$ .

   1. (i) If $f_{i}=0,$ then $g( 4i) =g( 8k+4) $ where from Theorem 1.5, \ i=2^{p}( 4h+3) .$ Since i is odd, $ p=0. $ Thus, $8k+4=4( 4h+3) $ and so $k=2h+1$ which is odd $.$ It follows that $g( 8k+4) =3$ for k odd.

   2. (ii) If $f_{i+1}=0,$ then $g( 4(i+1)) =g( 8k+8) $ where from Theorem 1.5, ${i+1=2^{m}( 4h+3) .}$ Since $i+1$ is even, $m>0.$ Thus, $8k+8=4( i+1) =2^{m+2} ( 4h+3) .$ That is, $k+1=2^{m-1}( 4h+3) =2^{p}( 4h+3) $ for $ p=m-1,$ that is, for $p\geq 0.$ It follows that $g( 8k+8) =3$ for $k+1=2^{p}( 4h+3) $ where $p\geq 0$ .

   3. (iii) If $f_{i}=1,$ then $g( 4i+1) =g( 8k+5) $ where from Theorem 1.5, $i=2^{p}( 4h+1) .$ Since i is odd, $p=0.$ Thus, $8k+5=4( 4h+1) +1$ and so $k=2h.$ It follows that $g( 8k+5) =3$ for k even.

   4. (iv) If $f_{i-1}=1,$ then for $i\geq 3,$ that is, $k\geq 1,\ g( 4( i-1) +1) =g( 4i-3) = g( 8k+1) $ where from Theorem 1.5 $\ i-1=2^{m}( 4h+1) .$ Since $i-1$ is even, $m>0.$ Thus, $8k+1=2^{m+2}( 4h+1) +1$ , that is, $ k=2^{m-1}( 4h+1) .$ It follows that $g( 8k+1) =3$ if $ k=2^{p}( 4h+1) $ for $p=m-1\geq 0.$

3. (3) $g( n) =2.$ Since the only possible terms in G are $1,\ 2$ and $3,$ all terms not part of conditions (i) and (ii) must be terms having value $2.$ The result follows.

The following theorem identifies important internal relationships within $G.$

Theorem 2.2 (Relationships in G).

Let $G=g( 1) g( 2) g( 3) \ldots $ be the summed paperfolding sequence of infinite length, then:

1. (a) $g( 2) =1,\ g( 2^{n}) =2$ for $n>1;$

2. (b) $g( 3) =2,\ g( 2^{n}+1) =3$ for $n>1;$

3. (c) $g( 2^{n}-i) =g( i+1) $ for $0\leq i<2^{n-1}-1;$

4. (d) $g( 2^{n}+i) =g( i) $ for $1<i<2^{n-1}$ or $ 2^{n-1}+1<i<2^{n}-1;$

5. (e) $g( 6) =2,\ g( 2^{n}+2^{n-1}) =3$ for $ n>2; $

6. (f) $g( 7) =1,\ g( 2^{n}+2^{n-1}+1) =2$ for $ n>2;$

7. (g) $g( 2^{n}+2^{m}) =g( 2^{m}) =2$ for $ n>m+1>2;$

8. (h) $g( 2^{n}+2^{m}+2^{r}) =g( 2^{m}+2^{r}) $ for $n>m+1>r+1;$

9. (i) $g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{2}}+2^{k_{3}}+\cdots +2^{k_{r}}) $ for $k_{1}>k_{2}>\cdots >k_{r}$ and $r>2;$

10. (j) $g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{r-2}}+2^{k_{r-1}}+2^{k_{r}}) $ for $k_{1}>k_{2}>\cdots >k_{r}$ and $r>2.$

Proof. The assertions follow from Theorem 2.1, with its subcases denoted by items (i) to (xii).

1. (a) $g( 2) =1$ by item (i); $g( 4) =2$ by item (v); $g(2^{n}) =2$ for $n>2$ by item (viii).

2. (b) $g( 3) =2$ by item (iv); $g( 5) =3$ by item (xi); $g( 2^{n}+1) =3$ for $n>2$ by item (ix).

3. (c) The first $2^{n-1}-1$ elements of $G_{n+1}$ are the sums of runs of $1$ and $0$ , and the last $2^{n-1}-1$ elements are the same sums, but of $0$ and $1$ and in reverse order. So, $g( 2^{n}-i) =g( i+1)$ for $0\leq i<2^{n-1}-1$ .

4. (d) As $2^{n}+i=2^{n+1}-( 2^{n}-i) $ if $1<i<2^{n-1},$ by part (c) applied twice,

   $$ \begin{align*} g( 2^{n}+i) =g( 2^{n}-( i-1) ) =g( i). \end{align*} $$
   If $2^{n-1}+1<i<2^{n}-1,$ then $i=2^{n-1}+2^{n-2}+\cdots +2^{r}+j,$ where either ${r=n-1}$ and $1<j<2^{r-1}-1$ or $r<n-1$ and $0\leq j<2^{r-1}-1.$ In both cases, by part (c),
   $$ \begin{align*} g( 2^{n}+i) =g( 2^{n+1}-( 2^{r}-j) ) =g( 2^{r}-( j-1) ) =g( 2^{n}-( 2^{r}-j) ) =g( i). \end{align*} $$

5. (e) $g( 6) =2$ by item (vii); $g( 12) =3$ by item (x); $g( 2^{n}+2^{n-1}) =g( 3.2^{n-1}) =3$ for ${n>3}$ and $ 2^{n-1}+1<i<2^{n}-1$ by item (xii).

6. (f) $g( 7) =1$ by item (ii), $g( 13) =2$ by item (vi); $g( 2^{n}+2^{n-1}+1) =g( 3.2^{n-1}+1) =2$ for $n>3$ by item (iii).

7. (g) For $p=n-m\geq 2,\ g( 2^{n}+2^{m}) =g( 2^{m}( 2^{p}+1) ) =2$ by item (viii) and $g( 2^{m}) =2$ if ${m=0,1}$ and $g( 2^{m}) =2$ if $m\geq 3$ by item (viii). Thus, if $n>m+1>2, g( 2^{n}+2^{m}) =g( 2^{m}) =2,$ by parts (d) and (a).

8. (h) For $n>m+1$ or $r>0,$ by item (viii),

   $$ \begin{align*} g( 2^{m}+2^{r}) =g( 2^{r}( 2^{m-r}+1) ) =g( 2^{r}( 4h_{0}+1) ) =2. \end{align*} $$
   For $n>m+1>r+1,$ by part (d) and item (viii),
   $$ \begin{align*} g( 2^{n}+2^{m}+2^{r}) & = g( 2^{r}( 2^{n-r}+(4h_{0}+1) ) )=g( 2^{r}( 4h_{1}+( 4h_{0}+1) ) )\\ & = g( 2^{r}( 4( h_{1}+h_{0}) +1) ) =2. \end{align*} $$

9. (i) For $r>2$ and $k_{1}>k_{2}>\cdots >k_{r}$ , by part (d),

   $$ \begin{align*} g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{2}}+2^{k_{3}}+\cdots +2^{k_{r}}). \end{align*} $$

10. (j) By repeated use of part (i) of this proof.

Note that for $n>1$ , $g(2^{n})=2$ and, for $n>2,\ g(2^{n})+1=3.$ This follows from observing that the sequence prior to $g(2^{n-1})$ is mirrored to give the sequence after $g(2^{n-1}+1)$ , reflected around $2,3$ in each case.

3. The expression $h(n)$

The following definition is important in developing our main result.

Definition 3.1 (Expression for $h(n)$ ).

For $n>0,$

$$ \begin{align*} h( n) =g( 1) +g( 2) +g( 3) +\cdots +g( n) . \end{align*} $$

Theorem 3.2 (Relationships involving $h(n))$ .

Assume $n>0$ .

1. (a) If $n=4q+1$ , then $h( n) =2n.$

2. (b) If $n=2^{k}( 4q+1) $ and $k>0$ , then $h( n) =2n-1.$

3. (c) If $n=4q+3$ , then $h( n) =2n-1.$

4. (d) If $n=2^{k}( 4q+3) $ and $k>0$ , then $h( n) =2n.$

Proof. The proof is by induction on $n.$ For $n=1,5$ and $6,\ h( n) =2n;$ and for $ n=2,3$ and $4,\ h( n) =2n-1.$ So conditions (a) to (d) hold for these minimal values of $n.$ Assume conditions (a) to (d) for values less than some $n.$ Suppose $ n=2^{k}( 4q+1)>3$ and let $q=\sum _{i=1}^{r}2^{q_{i}}.$ Then

$$ \begin{align*} n=2^{k}+\sum_{i=1}^{r}2^{q_{i}+k+2} \end{align*} $$

and

$$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +\sum_{j=1}^{n-2^{q_{1}+k+2}}g( 2^{q_{1}+k+2}+j). \end{align*} $$

If $q_{2}<q_{1}-1$ , then $n-2^{q_{1}+k+2}<2^{q_{1}+k+1},$ so by Theorem 2.2(b) and (d),

$$ \begin{align*} g( 2^{q_{1}+k+2}+1) = 3=g( 1) +1 \end{align*} $$

and

$$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +1+\sum_{j=1}^{n-2^{q_{1}+k+2}}g( j) =h( 2^{q_{1}+k+2}) +1+h( n-2^{q_{1}+k+2}). \end{align*} $$

So by the induction hypothesis, if $k>0,$

$$ \begin{align*} h( n) = 2^{q_{1}+k+3}-1+1+2n-2^{q_{1}+k+3}-1 = 2n-1. \end{align*} $$

If $q_{2}=q_{1}-1,$ by Theorem 2.2(e), (b) and (f),

$$ \begin{align*} g( 2^{q_{1}+k+2}+2^{q_{2}+k+2}) & =3=g( 2^{q_{2}+k+2})+1 \\ g( 2^{q_{1}+k+2}+2^{q_{2}+k+2}+1) & =2=g(2^{q_{2}+k+2}+1) -1. \end{align*} $$

So by Theorem 2.2 $(d)$ , for the other values of $j,$

$$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +1+\sum_{j=1}^{n-2^{q_{1}+k+2}}g( j) =2n-1 \end{align*} $$

as before, so we have condition (b). If, instead, $k=0,$ the induction hypothesis gives

$$ \begin{align*} h( n) =2^{q_{1}+k+3}-1+1+2n-2^{q_{1}+k+3} =2n, \end{align*} $$

then we have condition (a). If $n=2^{k}( 4q+3)$ , the working is as above, except that the induction hypothesis gives, for $k>0,$

$$ \begin{align*} h( n) =2^{q_{1}+k+3}-1+1+2n-2^{q_{1}+k+3} =2n, \end{align*} $$

and for $k=0,$

$$ \begin{align*} h( n) =2^{q_{1}+k+3}-1+1+2n-2^{q_{1}+k+3}-1 =2n-1, \end{align*} $$

so we have conditions (d) and (c).

Theorem 3.3 (Limits on $h(n)$ ).

If $h( n) +1\neq 2, 7\pmod 8$ , then $g( h( n) +1) =2$ and for no other values of m is $g( m) =2.$

Proof. If $n=4q+1,$ by Theorem 3.2(a), $h( n) +1=2n+1=8q+3$ . So by Theorem 2.1(iv), we have the result.

If $n=2^{k}( 4q+1) $ and $k>0,$ by Theorem 3.2(b), $h( n) +1=2n=2^{k+1}( 4q+1)$ and we have the result by Theorem 2.1(viii) if $k>1,$ and by Theorem 2.1(v) if $k=1.$

If $n=4q+3,$ by Theorem 3.2(c), $h( n) +1=2n=8q+6$ . So by Theorem 2.1(vii), we have the result.

If $n=2^{k}( 4q+3) ,$ by Theorem 3.2(d), $h( n) +1=2n+1=2^{k+3}q+2^{k+2}+2^{k+1}+1$ . So by Theorem 2.2(j), $g( h( n) +1) =g( 2^{k+2}+2^{k+1}+1)$ and the result follows from Theorem 2.2(f).

By Theorem 3.2, the value of $g( m) $ when ${m=8q+7}$ or $ 8q+2 $ is $1$ , and for ${m=8q+1,}\ 2^{k+1}( 4q+3) $ with $k>0$ or $ 2^{k+1}( 4q+1) +1$ with $k>0,\ g( m) =3.$

Summarising, $g( m) =2,$ where $m=8q+3,\ 8q+6,\ 2^{k+1}( 4q+1) $ with $k>0$ and $2^{k+1}( 4q+3) +1$ with $k>0.$ So all the cases when $g( m) =2$ are obtained when ${m=h( n) +1}.$

4. Confirmation of Hendriks’s conjecture

We are now able to state our main result, namely that the sequence $ {A=a( 1) a( 2) a( 3) \ldots } $ of A088431 is exactly the sequence $G=g( 1) g( 2) g( 3)\ldots .$

Theorem 4.1 (Confirmation of Hendriks’s conjecture).

The sequences A and G are the same, that is, $a( n) =g(n) $ .

Proof. By Theorem 2.2(c), $g( 2^{n}-i) =g( i)$ for $0\leq i<2^{n-1}-1,$ and

$$ \begin{align*} g( 2^{n}-2^{n-1}+1) =g( 2^{n-1}-1) =3=g( 2^{n-1}) +1. \end{align*} $$

Let $G_{n}^{R+1}$ denote the reverse of $G_{n}$ with a $1$ added to the new first term. Then

$$ \begin{align*} G_{n+1}=G_{n}G_{n}^{R+1}. \end{align*} $$

Since

$$ \begin{align*} G_{5}=2122321231232212, \end{align*} $$

$G_{5}$ has the subsequences: $321,123,1223,3221,212,312,232$ and $231.$ Thus, $321$ and $213$ will appear in $G_{5}^{R+1}$ and so in $G_{6}.$ For $ n>3,$

$$ \begin{align*} g( 2^{n-1}) =g( 2^{n-1}+2) =2 \quad\text{and}\quad g( 2^{n-1}+1) =3, \end{align*} $$

so the middle sequence of any $G_{n}$ will be $232.$ No new sequence of this kind can be generated in any $G_{n}$ or $G_{n}^{R+1}.$ Leaving out all the $ 2\mathrm{s}$ in $G,$ every $1$ is followed by a $3$ and every $3$ is followed by a $ 1,$ giving $1,3,1,3,\ldots .$ By Theorem 3.3, $\ g( n) $ has the defining properties of $a(n)$ given at Definition 1.2.

The referee advised us of the existence of the free software Walnut, which is described by Shallit [12]. Walnut can decide first-order predicates about automatic sequences, including the paperfolding sequence. The referee confirmed Theorem 4.1 using Walnut code. Walnut is authored by Hamoon Mousavi, and has been used extensively in confirming features of sequences found in the Online Encyclopedia of Integer Sequences (OEIS).

5. Summed paperfolding and continued fractions

There is an interesting connection between continued fractions and summed paperfolding. Shallit [11] identifies the continued fraction expansion of $\sum _{k=0}^{u+1}{1}/{m^{2^{k}}}$ for m an integer greater than $1$ , once the continued fraction expansion of $\sum _{k=0}^{u} {1}/{m^{2^{k}}}$ is known. Thus, if

$$ \begin{align*} \sum_{k=0}^{u}\frac{1}{m^{2^{k}}}=[a_{0};a_{1},\ldots ,a_{n}], \end{align*} $$

then

$$ \begin{align*} \sum_{k=0}^{u+1}\frac{1}{m^{2^{k}}}=[a_{0};a_{1},\ldots ,a_{n-1},a_{n}+1,a_{n}-1,a_{n}-1,a_{n-1},a_{n-2},\ldots ,a_{2},a_{1}]. \end{align*} $$

He acknowledges that for $m=2,$ which is the focus of our attention, the expansion contains a number of terms having value $0.$ This is not problematic as the following equality allows for the conversion of such continued fractions:

$$ \begin{align*} \lbrack a_{0};a_{1},\ldots ,a_{i},0,a_{i+1},a_{i+2},\ldots ,a_{n}]=[a_{0};a_{1},\ldots ,a_{i}+a_{i+1},a_{i+2},\ldots ,a_{n}]. \end{align*} $$

He also shows that $\sum _{k=0}^{\infty }1/m^{2^k}$ for $m\geq 2$ is irrational and proves some interesting results relating to the partial denominators of its continued fraction.

Pethö [10] generalises the method found by Shallit [11] to develop a continued fraction expansion for Fredholm numbers of the second kind. The number $\sum _{k=0}^{\infty }{1}/{2^{2^{k}}},$ upon which the summed paperfolding sequence is based, is an example of a Fredholm number of the second kind.