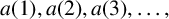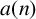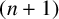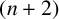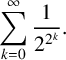1. Introduction and preliminaries
According to Ben-Abraham et al. [Reference Ben-Abraham, Quandt and Shapira4], the regular paperfolding sequence was discovered in the mid-1960s by three NASA physicists: John Heighway, Bruce Banks and William Hartner. Martin Gardner celebrated their work in Scientific American [Reference Gardner7], after which Davis and Knuth [Reference Davis and Knuth5] developed the mathematical underpinnings of paperfolding. Since that time, many papers have been written exploring the diverse features of this sequence, notably Dekking et al. [Reference Dekking, Mendes France and van der Poorten6], Allouche and Shallit [Reference Allouche and Shallit1], Mendès France and van der Poorten [Reference Mendès France and van der Poorten9], and Mendès France and Shallit [Reference Mendès France and Shallit8].
We start with two alternative definitions of sequence A088431, both found in the Online Encyclopedia of Integer Sequences [Reference Sloane13].
Definition 1.1 (A088431 continued fraction definition [Reference Sloane13]).
The sequence
![]() $ {A=a( 1) a( 2) a( 3) \ldots }$
is defined by:
$ {A=a( 1) a( 2) a( 3) \ldots }$
is defined by:
![]() $a( n) $
is half of the
$a( n) $
is half of the
![]() $ ( n+1) $
th component, that is, the
$ ( n+1) $
th component, that is, the
![]() $( n+2) $
th term, of the continued fraction expansion of
$( n+2) $
th term, of the continued fraction expansion of
 $$ \begin{align*} \sum_{k=0}^{\infty }\frac{1}{2^{2^{k}}}. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{\infty }\frac{1}{2^{2^{k}}}. \end{align*} $$
Definition 1.2 (A088431 alternative definition [Reference Sloane13]).
The sequence
![]() ${A=a( 1) a( 2) a( 3) \ldots } $
is given by the following rule: let
${A=a( 1) a( 2) a( 3) \ldots } $
is given by the following rule: let
![]() $ i=1,2,3,\ldots $
and
$ i=1,2,3,\ldots $
and
![]() $a( 1) =2.$
Then
$a( 1) =2.$
Then
and the ith undefined term of A is the ith term of the sequence
Example 1.3. Based on Definition 1.2, we give the first few terms of the sequence A088431 in Table 1.
Table 1 Initial terms of the sequence A088431.

Dimitri Hendriks in [Reference Sloane13] has suggested that sequence A088431 appears to be the sequence of run lengths of the regular paperfolding sequence A014577. We prove several results concerning this summed paperfolding sequence and confirm Hendriks’s conjecture.
In what follows, for simplicity and where no ambiguity exists, we remove the commas from sequences. For example, for a sequence only having values
![]() $1,2$
or
$1,2$
or
![]() $3,$
the sequence
$3,$
the sequence
![]() $2,2,1,3$
becomes
$2,2,1,3$
becomes
![]() $2213.$
$2213.$
Davis and Knuth [Reference Davis and Knuth5] prove the following result which we adopt as a definition for the paperfolding sequence. The notation is taken from Bates et al. [Reference Bates, Bunder and Tognetti2].
Definition 1.4 (Paperfolding sequence).
Let
![]() $S_{n}$
be the paperfolding sequence of length
$S_{n}$
be the paperfolding sequence of length
![]() $2^{n}-1$
and let
$2^{n}-1$
and let
![]() $\overline {\text { }S_{n}^{R}}$
be
$\overline {\text { }S_{n}^{R}}$
be
![]() $S_{n}$
in reverse order with
$S_{n}$
in reverse order with
![]() $0$
becoming
$0$
becoming
![]() $1$
and
$1$
and
![]() $1$
becoming
$1$
becoming
![]() $0$
. Then,
$0$
. Then,
![]() $ S_{1}=1,\label {zd} S_{n+1} =S_{n}1\overline {S_{n}^{R}}$
and
$ S_{1}=1,\label {zd} S_{n+1} =S_{n}1\overline {S_{n}^{R}}$
and
![]() $\overline {S_{n+1}^{R}} =S_{n}0\overline {\text { }S_{n}^{R}}$
.
$\overline {S_{n+1}^{R}} =S_{n}0\overline {\text { }S_{n}^{R}}$
.
Bates et al. [Reference Bates, Bunder and Tognetti2, Reference Bates, Bunder and Tognetti3] identify the following results for
![]() $ S_{n}$
.
$ S_{n}$
.
Theorem 1.5 (Expression for
 $S_{n}$
).
$S_{n}$
).
For
![]() $n>0$
and
$n>0$
and
![]() $h,k\geq 0$
,
$h,k\geq 0$
,
![]() $ S_{n}=f_{1}f_{2}\ldots f_{2^{n}-1}$
, where
$ S_{n}=f_{1}f_{2}\ldots f_{2^{n}-1}$
, where
 $$ \begin{align*} f_{i}=\left\{ \begin{array}{@{}ll} 1 &\text{if }i=2^{k}(4h+1), \\ 0 &\text{if }i=2^{k}(4h+3). \end{array} \right. \end{align*} $$
$$ \begin{align*} f_{i}=\left\{ \begin{array}{@{}ll} 1 &\text{if }i=2^{k}(4h+1), \\ 0 &\text{if }i=2^{k}(4h+3). \end{array} \right. \end{align*} $$
Theorem 1.6 (Paperfolding runs).
The paperfolding sequence,
![]() $S_{n}$
, contains only runs of single, double or triple entries of
$S_{n}$
, contains only runs of single, double or triple entries of
![]() $0;$
or single, double or triple entries of
$0;$
or single, double or triple entries of
![]() $1.$
In particular, for
$1.$
In particular, for
![]() $n\geq 4,\ S_{n}$
contains:
$n\geq 4,\ S_{n}$
contains:
-
(i)
 $2^{n-4}$
instances of the triple
$2^{n-4}$
instances of the triple
 $111,$
and
$111,$
and
 $2^{n-4}-1$
instances of the triple
$2^{n-4}-1$
instances of the triple
 $000;$
$000;$
-
(ii)
 $2^{n-3}$
instances of the double
$2^{n-3}$
instances of the double
 $11,$
and
$11,$
and
 $2^{n-3}+1$
instances of the double
$2^{n-3}+1$
instances of the double
 $00;$
$00;$
-
(iii)
 $2^{n-4}$
instances each of the single
$2^{n-4}$
instances each of the single
 $1,$
and the single
$1,$
and the single
 $0.$
$0.$
Theorem 1.7 (Interleaved paperfolding).
Let
![]() $S=f_{1}f_{2}f_{3}\ldots $
be the paperfolding sequence of infinite length. Then
$S=f_{1}f_{2}f_{3}\ldots $
be the paperfolding sequence of infinite length. Then
That is, S is formed from the alternating interleave of two subsequences,
![]() $ S_{3}$
and
$ S_{3}$
and
![]() $\overline {\text { }S_{3}^{R}},$
with itself.
$\overline {\text { }S_{3}^{R}},$
with itself.
![]() $\label {o}$
$\label {o}$
We consider the runs of identical terms in
![]() $S_{n}$
or
$S_{n}$
or
![]() $S,$
that is, the sizes of the sequence of successive digits
$S,$
that is, the sizes of the sequence of successive digits
![]() $1$
and
$1$
and
![]() $0$
of
$0$
of
![]() $S_{n}$
or
$S_{n}$
or
![]() $S.$
We begin with a definition of these runs.
$S.$
We begin with a definition of these runs.
Definition 1.8 (Summed paperfolding sequence).
For
![]() $S_{n}=f_{1}f_{2}\ldots f_{2^{n}-1}$
:
$S_{n}=f_{1}f_{2}\ldots f_{2^{n}-1}$
:
-
• the summed paperfolding sequence,
 $G_{n}$
, is the sequence of the sizes of successive digits
$G_{n}$
, is the sequence of the sizes of successive digits
 $1$
and
$1$
and
 $0$
of
$0$
of
 $S_{n};$
$S_{n};$
-
• the summed paperfolding sequence of infinite length is
 $ G=\lim _{n\rightarrow \infty }\ G_{n}$
and is designated as
$ G=\lim _{n\rightarrow \infty }\ G_{n}$
and is designated as
 $G=g( 1) g( 2) g( 3) \ldots $
$G=g( 1) g( 2) g( 3) \ldots $
We show in Theorem 1.10 that
![]() $G_{n}$
has length
$G_{n}$
has length
![]() $2^{n-1}.$
$2^{n-1}.$
Example 1.9.
![]() $S_{4} =110110011100100, G_{4} =21223212$
and
$S_{4} =110110011100100, G_{4} =21223212$
and
![]() $G =21223212\ldots .$
$G =21223212\ldots .$
The key results in this paper are:
-
• Theorem 2.1, a closed-form expression for G analogous to the expression for
 $S_{n}$
(and by extension
$S_{n}$
(and by extension
 $S)$
given at Theorem 1.5;
$S)$
given at Theorem 1.5; -
• Theorem 2.2 identifying the main internal relationships within G;
-
• Theorem 4.1 (Main Result) confirming Hendriks’s conjecture [Reference Sloane13]. That is, the sequence
 $A=a( 1) a( 2) a( 3) \ldots $
of A088431 is exactly the sequence
$A=a( 1) a( 2) a( 3) \ldots $
of A088431 is exactly the sequence
 ${G=g( 1) g( 2) g( 3) \ldots } $
of Definition 1.8.
${G=g( 1) g( 2) g( 3) \ldots } $
of Definition 1.8.
Theorem 1.10 (Length of
 $G_{n}$
).
$G_{n}$
).
![]() $\vert G_{n}\vert =2^{n-1}, $
where
$\vert G_{n}\vert =2^{n-1}, $
where
![]() $\vert G_{n}\vert $
is the length of
$\vert G_{n}\vert $
is the length of
![]() $G_{n}. \label {ze}$
$G_{n}. \label {ze}$
Proof. For
![]() $n<4$
, our result is true. From Theorem 1.6, for
$n<4$
, our result is true. From Theorem 1.6, for
![]() $n\geq 4,$
there are
$n\geq 4,$
there are
![]() $2^{n-4}\ 111\mathrm{s}$
,
$2^{n-4}\ 111\mathrm{s}$
,
![]() $2^{n-4}-1\ 000\mathrm{s}$
,
$2^{n-4}-1\ 000\mathrm{s}$
,
![]() $2^{n-3}\ 11\mathrm{s}$
,
$2^{n-3}\ 11\mathrm{s}$
,
![]() $2^{n-3}+1\ 00\mathrm{s}$
,
$2^{n-3}+1\ 00\mathrm{s}$
,
![]() $2^{n-4}\ 1\mathrm{s}$
and
$2^{n-4}\ 1\mathrm{s}$
and
![]() $2^{n-4}\ 0\mathrm{s}$
. Hence,
$2^{n-4}\ 0\mathrm{s}$
. Hence,
Note that from Definition 1.4, since
![]() $S_{n+1}=S_{n}1\overline {S_{n}^{R}} ,$
the initial
$S_{n+1}=S_{n}1\overline {S_{n}^{R}} ,$
the initial
![]() $\vert G_{n}\vert $
terms of
$\vert G_{n}\vert $
terms of
![]() $G_{n+1}$
will be
$G_{n+1}$
will be
![]() $ G_{n}.$
Since by Theorem 1.10,
$ G_{n}.$
Since by Theorem 1.10,
![]() $\vert G_{n}\vert =2^{n-1}$
, we can write
$\vert G_{n}\vert =2^{n-1}$
, we can write
2. Basic facts concerning G
We now develop an analogous expression for G to that given at Theorem 1.5 for
![]() $S_{n}$
(and, by extension, S).
$S_{n}$
(and, by extension, S).
Theorem 2.1 (Expression for G).
For
![]() $h,k,p\geq 0$
,
$h,k,p\geq 0$
,
![]() $G=g( 1) g( 2) g( 3) \ldots ,$
where
$G=g( 1) g( 2) g( 3) \ldots ,$
where
 $$ \begin{align*} g( n) = \begin{cases} 1\text{ if (i) }n=8k+2\text{, or } \\\quad\ \text{if (ii) }n=8k+7, \\2\text{ if (iii) }n=8k+1\text{ and }k=2^{p}( 4h+3),\text{ or} \\\quad\ \text{if (iv) }n=8k+3,\text{ or} \\\quad\ \text{if (v) }n=8k+4\text{ and }k\text{ is even},\text{ or} \\\quad\ \text{if (vi) }n=8k+5\text{ and }k\text{ is odd, or} \\\quad\ \text{if (vii) }n=8k+6\text{, or} \\\quad\ \text{if (viii) }n=8k+8\text{ and }k+1=2^{p}( 4h+1). \\3\text{ if (ix) }n=8k+1\text{ and }k=2^{p}( 4h+1) ,\text{ or} \\\quad\ \text{if (x) }n=8k+4\text{ and }k\text{ is odd, or} \\\quad\ \text{if (xi) }n=8k+5\text{ and }k\text{ is even, or} \\\quad\ \text{if (xii) }n=8k+8\text{ and }k+1=2^{p}( 4h+3) \text{.} \end{cases} \end{align*} $$
$$ \begin{align*} g( n) = \begin{cases} 1\text{ if (i) }n=8k+2\text{, or } \\\quad\ \text{if (ii) }n=8k+7, \\2\text{ if (iii) }n=8k+1\text{ and }k=2^{p}( 4h+3),\text{ or} \\\quad\ \text{if (iv) }n=8k+3,\text{ or} \\\quad\ \text{if (v) }n=8k+4\text{ and }k\text{ is even},\text{ or} \\\quad\ \text{if (vi) }n=8k+5\text{ and }k\text{ is odd, or} \\\quad\ \text{if (vii) }n=8k+6\text{, or} \\\quad\ \text{if (viii) }n=8k+8\text{ and }k+1=2^{p}( 4h+1). \\3\text{ if (ix) }n=8k+1\text{ and }k=2^{p}( 4h+1) ,\text{ or} \\\quad\ \text{if (x) }n=8k+4\text{ and }k\text{ is odd, or} \\\quad\ \text{if (xi) }n=8k+5\text{ and }k\text{ is even, or} \\\quad\ \text{if (xii) }n=8k+8\text{ and }k+1=2^{p}( 4h+3) \text{.} \end{cases} \end{align*} $$
Proof. From Theorem 1.6, S only contains singles, doubles and triples. Thus, the only possible terms in G are
![]() $1,\ 2$
and
$1,\ 2$
and
![]() $3.$
From Theorem 1.7, each
$3.$
From Theorem 1.7, each
![]() $S_{3}$
and
$S_{3}$
and
![]() $\overline {\text { }S_{3}^{R}}$
starts with
$\overline {\text { }S_{3}^{R}}$
starts with
![]() $11$
and ends with
$11$
and ends with
![]() $00$
and the component
$00$
and the component
![]() $S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
is followed by
$S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
is followed by
![]() $S_{3}\ f_{i+2}\overline {\text { }S_{3}^{R}}\ f_{i+3},$
which is followed by
$S_{3}\ f_{i+2}\overline {\text { }S_{3}^{R}}\ f_{i+3},$
which is followed by
![]() $S_{3}\ f_{i+4}\overline {\text { }S_{3}^{R}}\ f_{i+5},$
and so on, indefinitely. Let the
$S_{3}\ f_{i+4}\overline {\text { }S_{3}^{R}}\ f_{i+5},$
and so on, indefinitely. Let the
![]() $0$
th component be
$0$
th component be
![]() $S_{3}\ f_{1} \overline {\text { }S_{3}^{R}}\ f_{2}.$
Then the kth component is
$S_{3}\ f_{1} \overline {\text { }S_{3}^{R}}\ f_{2}.$
Then the kth component is
![]() $S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
where i is odd and
$S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
where i is odd and
![]() ${k={(i-1)}/{2}}$
. Thus, the translation from S to G of the kth component,
${k={(i-1)}/{2}}$
. Thus, the translation from S to G of the kth component,
![]() $ S_{3} \ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1},$
can be represented by eight terms,
$ S_{3} \ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1},$
can be represented by eight terms,
![]() $g( 8k+1) $
to
$g( 8k+1) $
to
![]() $g( 8k+8) ,$
where
$g( 8k+8) ,$
where
![]() $k={(i-1)}/{2}$
with two possible configurations:
$k={(i-1)}/{2}$
with two possible configurations:
-
•
 $f_{i}=0:\ S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
becomes (
$f_{i}=0:\ S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
becomes (
 $2$
or
$2$
or
 $3)123221(2$
or
$3)123221(2$
or
 $3);$
or
$3);$
or -
•
 $f_{i}=1:\ S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
becomes (
$f_{i}=1:\ S_{3}\ f_{i}\overline {\text { }S_{3}^{R}}\ f_{i+1}$
becomes (
 $2$
or
$2$
or
 $3)122321(2$
or
$3)122321(2$
or
 $3)$
,
$3)$
,
where bracketed entries are determined by the values of
![]() $f_{i-1}$
and
$f_{i-1}$
and
![]() $ f_{i+1}.$
$ f_{i+1}.$
We consider each of
![]() $g( n) =1,\ 3$
and
$g( n) =1,\ 3$
and
![]() $2$
separately.
$2$
separately.
-
(1)
 $g( n) =1.$
In the
$g( n) =1.$
In the
 $8$
-term translations above, we have
$8$
-term translations above, we have
 $ g( 8k+2) $
and
$ g( 8k+2) $
and
 $g( 8k+7) $
always taking the value
$g( 8k+7) $
always taking the value
 $1,$
irrespective of the values of
$1,$
irrespective of the values of
 $f_{i-1},f_{i}$
or
$f_{i-1},f_{i}$
or
 $f_{i+1},$
and there are no other values of
$f_{i+1},$
and there are no other values of
 $1$
in this
$1$
in this
 $8$
-term translation. Thus,
$8$
-term translation. Thus,
 $g( n) =1$
if
$g( n) =1$
if
 $n=8k+2$
or
$n=8k+2$
or
 $8k+7.$
$8k+7.$
-
(2)
 $g( n) =3.$
Consider the component
$g( n) =3.$
Consider the component
 $S_{3}\ f_{i}\overline { \text { }S_{3}^{R}}\ f_{i+1}$
.
$S_{3}\ f_{i}\overline { \text { }S_{3}^{R}}\ f_{i+1}$
.-
(i) If
 $f_{i}=0,$
then
$f_{i}=0,$
then
 $g( 4i) =g( 8k+4) $
where from Theorem 1.5,
$g( 4i) =g( 8k+4) $
where from Theorem 1.5,
 \ i=2^{p}( 4h+3) .$
Since i is odd,
\ i=2^{p}( 4h+3) .$
Since i is odd,
 $ p=0. $
Thus,
$ p=0. $
Thus,
 $8k+4=4( 4h+3) $
and so
$8k+4=4( 4h+3) $
and so
 $k=2h+1$
which is odd
$k=2h+1$
which is odd
 $.$
It follows that
$.$
It follows that
 $g( 8k+4) =3$
for k odd.
$g( 8k+4) =3$
for k odd. -
(ii) If
 $f_{i+1}=0,$
then
$f_{i+1}=0,$
then
 $g( 4(i+1)) =g( 8k+8) $
where from Theorem 1.5,
$g( 4(i+1)) =g( 8k+8) $
where from Theorem 1.5,
 ${i+1=2^{m}( 4h+3) .}$
Since
${i+1=2^{m}( 4h+3) .}$
Since
 $i+1$
is even,
$i+1$
is even,
 $m>0.$
Thus,
$m>0.$
Thus,
 $8k+8=4( i+1) =2^{m+2} ( 4h+3) .$
That is,
$8k+8=4( i+1) =2^{m+2} ( 4h+3) .$
That is,
 $k+1=2^{m-1}( 4h+3) =2^{p}( 4h+3) $
for
$k+1=2^{m-1}( 4h+3) =2^{p}( 4h+3) $
for
 $ p=m-1,$
that is, for
$ p=m-1,$
that is, for
 $p\geq 0.$
It follows that
$p\geq 0.$
It follows that
 $g( 8k+8) =3$
for
$g( 8k+8) =3$
for
 $k+1=2^{p}( 4h+3) $
where
$k+1=2^{p}( 4h+3) $
where
 $p\geq 0$
.
$p\geq 0$
. -
(iii) If
 $f_{i}=1,$
then
$f_{i}=1,$
then
 $g( 4i+1) =g( 8k+5) $
where from Theorem 1.5,
$g( 4i+1) =g( 8k+5) $
where from Theorem 1.5,
 $i=2^{p}( 4h+1) .$
Since i is odd,
$i=2^{p}( 4h+1) .$
Since i is odd,
 $p=0.$
Thus,
$p=0.$
Thus,
 $8k+5=4( 4h+1) +1$
and so
$8k+5=4( 4h+1) +1$
and so
 $k=2h.$
It follows that
$k=2h.$
It follows that
 $g( 8k+5) =3$
for k even.
$g( 8k+5) =3$
for k even. -
(iv) If
 $f_{i-1}=1,$
then for
$f_{i-1}=1,$
then for
 $i\geq 3,$
that is,
$i\geq 3,$
that is,
 $k\geq 1,\ g( 4( i-1) +1) =g( 4i-3) = g( 8k+1) $
where from Theorem 1.5
$k\geq 1,\ g( 4( i-1) +1) =g( 4i-3) = g( 8k+1) $
where from Theorem 1.5
 $\ i-1=2^{m}( 4h+1) .$
Since
$\ i-1=2^{m}( 4h+1) .$
Since
 $i-1$
is even,
$i-1$
is even,
 $m>0.$
Thus,
$m>0.$
Thus,
 $8k+1=2^{m+2}( 4h+1) +1$
, that is,
$8k+1=2^{m+2}( 4h+1) +1$
, that is,
 $ k=2^{m-1}( 4h+1) .$
It follows that
$ k=2^{m-1}( 4h+1) .$
It follows that
 $g( 8k+1) =3$
if
$g( 8k+1) =3$
if
 $ k=2^{p}( 4h+1) $
for
$ k=2^{p}( 4h+1) $
for
 $p=m-1\geq 0.$
$p=m-1\geq 0.$
-
-
(3)
 $g( n) =2.$
Since the only possible terms in G are
$g( n) =2.$
Since the only possible terms in G are
 $1,\ 2$
and
$1,\ 2$
and
 $3,$
all terms not part of conditions (i) and (ii) must be terms having value
$3,$
all terms not part of conditions (i) and (ii) must be terms having value
 $2.$
The result follows.
$2.$
The result follows.
The following theorem identifies important internal relationships within
![]() $G.$
$G.$
Theorem 2.2 (Relationships in G).
Let
![]() $G=g( 1) g( 2) g( 3) \ldots $
be the summed paperfolding sequence of infinite length, then:
$G=g( 1) g( 2) g( 3) \ldots $
be the summed paperfolding sequence of infinite length, then:
-
(a)
 $g( 2) =1,\ g( 2^{n}) =2$
for
$g( 2) =1,\ g( 2^{n}) =2$
for
 $n>1;$
$n>1;$
-
(b)
 $g( 3) =2,\ g( 2^{n}+1) =3$
for
$g( 3) =2,\ g( 2^{n}+1) =3$
for
 $n>1;$
$n>1;$
-
(c)
 $g( 2^{n}-i) =g( i+1) $
for
$g( 2^{n}-i) =g( i+1) $
for
 $0\leq i<2^{n-1}-1;$
$0\leq i<2^{n-1}-1;$
-
(d)
 $g( 2^{n}+i) =g( i) $
for
$g( 2^{n}+i) =g( i) $
for
 $1<i<2^{n-1}$
or
$1<i<2^{n-1}$
or
 $ 2^{n-1}+1<i<2^{n}-1;$
$ 2^{n-1}+1<i<2^{n}-1;$
-
(e)
 $g( 6) =2,\ g( 2^{n}+2^{n-1}) =3$
for
$g( 6) =2,\ g( 2^{n}+2^{n-1}) =3$
for
 $ n>2; $
$ n>2; $
-
(f)
 $g( 7) =1,\ g( 2^{n}+2^{n-1}+1) =2$
for
$g( 7) =1,\ g( 2^{n}+2^{n-1}+1) =2$
for
 $ n>2;$
$ n>2;$
-
(g)
 $g( 2^{n}+2^{m}) =g( 2^{m}) =2$
for
$g( 2^{n}+2^{m}) =g( 2^{m}) =2$
for
 $ n>m+1>2;$
$ n>m+1>2;$
-
(h)
 $g( 2^{n}+2^{m}+2^{r}) =g( 2^{m}+2^{r}) $
for
$g( 2^{n}+2^{m}+2^{r}) =g( 2^{m}+2^{r}) $
for
 $n>m+1>r+1;$
$n>m+1>r+1;$
-
(i)
 $g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{2}}+2^{k_{3}}+\cdots +2^{k_{r}}) $
for
$g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{2}}+2^{k_{3}}+\cdots +2^{k_{r}}) $
for
 $k_{1}>k_{2}>\cdots >k_{r}$
and
$k_{1}>k_{2}>\cdots >k_{r}$
and
 $r>2;$
$r>2;$
-
(j)
 $g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{r-2}}+2^{k_{r-1}}+2^{k_{r}}) $
for
$g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{r-2}}+2^{k_{r-1}}+2^{k_{r}}) $
for
 $k_{1}>k_{2}>\cdots >k_{r}$
and
$k_{1}>k_{2}>\cdots >k_{r}$
and
 $r>2.$
$r>2.$
Proof. The assertions follow from Theorem 2.1, with its subcases denoted by items (i) to (xii).
-
(a)
 $g( 2) =1$
by item (i);
$g( 2) =1$
by item (i);
 $g( 4) =2$
by item (v);
$g( 4) =2$
by item (v);
 $g(2^{n}) =2$
for
$g(2^{n}) =2$
for
 $n>2$
by item (viii).
$n>2$
by item (viii). -
(b)
 $g( 3) =2$
by item (iv);
$g( 3) =2$
by item (iv);
 $g( 5) =3$
by item (xi);
$g( 5) =3$
by item (xi);
 $g( 2^{n}+1) =3$
for
$g( 2^{n}+1) =3$
for
 $n>2$
by item (ix).
$n>2$
by item (ix). -
(c) The first
 $2^{n-1}-1$
elements of
$2^{n-1}-1$
elements of
 $G_{n+1}$
are the sums of runs of
$G_{n+1}$
are the sums of runs of
 $1$
and
$1$
and
 $0$
, and the last
$0$
, and the last
 $2^{n-1}-1$
elements are the same sums, but of
$2^{n-1}-1$
elements are the same sums, but of
 $0$
and
$0$
and
 $1$
and in reverse order. So,
$1$
and in reverse order. So,
 $g( 2^{n}-i) =g( i+1)$
for
$g( 2^{n}-i) =g( i+1)$
for
 $0\leq i<2^{n-1}-1$
.
$0\leq i<2^{n-1}-1$
. -
(d) As
 $2^{n}+i=2^{n+1}-( 2^{n}-i) $
if
$2^{n}+i=2^{n+1}-( 2^{n}-i) $
if
 $1<i<2^{n-1},$
by part (c) applied twice, If
$1<i<2^{n-1},$
by part (c) applied twice, If $$ \begin{align*} g( 2^{n}+i) =g( 2^{n}-( i-1) ) =g( i). \end{align*} $$
$$ \begin{align*} g( 2^{n}+i) =g( 2^{n}-( i-1) ) =g( i). \end{align*} $$
 $2^{n-1}+1<i<2^{n}-1,$
then
$2^{n-1}+1<i<2^{n}-1,$
then
 $i=2^{n-1}+2^{n-2}+\cdots +2^{r}+j,$
where either
$i=2^{n-1}+2^{n-2}+\cdots +2^{r}+j,$
where either
 ${r=n-1}$
and
${r=n-1}$
and
 $1<j<2^{r-1}-1$
or
$1<j<2^{r-1}-1$
or
 $r<n-1$
and
$r<n-1$
and
 $0\leq j<2^{r-1}-1.$
In both cases, by part (c),
$0\leq j<2^{r-1}-1.$
In both cases, by part (c),  $$ \begin{align*} g( 2^{n}+i) =g( 2^{n+1}-( 2^{r}-j) ) =g( 2^{r}-( j-1) ) =g( 2^{n}-( 2^{r}-j) ) =g( i). \end{align*} $$
$$ \begin{align*} g( 2^{n}+i) =g( 2^{n+1}-( 2^{r}-j) ) =g( 2^{r}-( j-1) ) =g( 2^{n}-( 2^{r}-j) ) =g( i). \end{align*} $$
-
(e)
 $g( 6) =2$
by item (vii);
$g( 6) =2$
by item (vii);
 $g( 12) =3$
by item (x);
$g( 12) =3$
by item (x);
 $g( 2^{n}+2^{n-1}) =g( 3.2^{n-1}) =3$
for
$g( 2^{n}+2^{n-1}) =g( 3.2^{n-1}) =3$
for
 ${n>3}$
and
${n>3}$
and
 $ 2^{n-1}+1<i<2^{n}-1$
by item (xii).
$ 2^{n-1}+1<i<2^{n}-1$
by item (xii). -
(f)
 $g( 7) =1$
by item (ii),
$g( 7) =1$
by item (ii),
 $g( 13) =2$
by item (vi);
$g( 13) =2$
by item (vi);
 $g( 2^{n}+2^{n-1}+1) =g( 3.2^{n-1}+1) =2$
for
$g( 2^{n}+2^{n-1}+1) =g( 3.2^{n-1}+1) =2$
for
 $n>3$
by item (iii).
$n>3$
by item (iii). -
(g) For
 $p=n-m\geq 2,\ g( 2^{n}+2^{m}) =g( 2^{m}( 2^{p}+1) ) =2$
by item (viii) and
$p=n-m\geq 2,\ g( 2^{n}+2^{m}) =g( 2^{m}( 2^{p}+1) ) =2$
by item (viii) and
 $g( 2^{m}) =2$
if
$g( 2^{m}) =2$
if
 ${m=0,1}$
and
${m=0,1}$
and
 $g( 2^{m}) =2$
if
$g( 2^{m}) =2$
if
 $m\geq 3$
by item (viii). Thus, if
$m\geq 3$
by item (viii). Thus, if
 $n>m+1>2, g( 2^{n}+2^{m}) =g( 2^{m}) =2,$
by parts (d) and (a).
$n>m+1>2, g( 2^{n}+2^{m}) =g( 2^{m}) =2,$
by parts (d) and (a). -
(h) For
 $n>m+1$
or
$n>m+1$
or
 $r>0,$
by item (viii), For
$r>0,$
by item (viii), For $$ \begin{align*} g( 2^{m}+2^{r}) =g( 2^{r}( 2^{m-r}+1) ) =g( 2^{r}( 4h_{0}+1) ) =2. \end{align*} $$
$$ \begin{align*} g( 2^{m}+2^{r}) =g( 2^{r}( 2^{m-r}+1) ) =g( 2^{r}( 4h_{0}+1) ) =2. \end{align*} $$
 $n>m+1>r+1,$
by part (d) and item (viii),
$n>m+1>r+1,$
by part (d) and item (viii),  $$ \begin{align*} g( 2^{n}+2^{m}+2^{r}) & = g( 2^{r}( 2^{n-r}+(4h_{0}+1) ) )=g( 2^{r}( 4h_{1}+( 4h_{0}+1) ) )\\ & = g( 2^{r}( 4( h_{1}+h_{0}) +1) ) =2. \end{align*} $$
$$ \begin{align*} g( 2^{n}+2^{m}+2^{r}) & = g( 2^{r}( 2^{n-r}+(4h_{0}+1) ) )=g( 2^{r}( 4h_{1}+( 4h_{0}+1) ) )\\ & = g( 2^{r}( 4( h_{1}+h_{0}) +1) ) =2. \end{align*} $$
-
(i) For
 $r>2$
and
$r>2$
and
 $k_{1}>k_{2}>\cdots >k_{r}$
, by part (d),
$k_{1}>k_{2}>\cdots >k_{r}$
, by part (d),  $$ \begin{align*} g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{2}}+2^{k_{3}}+\cdots +2^{k_{r}}). \end{align*} $$
$$ \begin{align*} g( 2^{k_{1}}+2^{k_{2}}+\cdots +2^{k_{r}}) =g( 2^{k_{2}}+2^{k_{3}}+\cdots +2^{k_{r}}). \end{align*} $$
-
(j) By repeated use of part (i) of this proof.
Note that for
![]() $n>1$
,
$n>1$
,
![]() $g(2^{n})=2$
and, for
$g(2^{n})=2$
and, for
![]() $n>2,\ g(2^{n})+1=3.$
This follows from observing that the sequence prior to
$n>2,\ g(2^{n})+1=3.$
This follows from observing that the sequence prior to
![]() $g(2^{n-1})$
is mirrored to give the sequence after
$g(2^{n-1})$
is mirrored to give the sequence after
![]() $g(2^{n-1}+1)$
, reflected around
$g(2^{n-1}+1)$
, reflected around
![]() $2,3$
in each case.
$2,3$
in each case.
3. The expression
 $h(n)$
$h(n)$
The following definition is important in developing our main result.
Definition 3.1 (Expression for
 $h(n)$
).
$h(n)$
).
For
![]() $n>0,$
$n>0,$
Theorem 3.2 (Relationships involving
 $h(n))$
.
$h(n))$
.
Assume
![]() $n>0$
.
$n>0$
.
-
(a) If
 $n=4q+1$
, then
$n=4q+1$
, then
 $h( n) =2n.$
$h( n) =2n.$
-
(b) If
 $n=2^{k}( 4q+1) $
and
$n=2^{k}( 4q+1) $
and
 $k>0$
, then
$k>0$
, then
 $h( n) =2n-1.$
$h( n) =2n-1.$
-
(c) If
 $n=4q+3$
, then
$n=4q+3$
, then
 $h( n) =2n-1.$
$h( n) =2n-1.$
-
(d) If
 $n=2^{k}( 4q+3) $
and
$n=2^{k}( 4q+3) $
and
 $k>0$
, then
$k>0$
, then
 $h( n) =2n.$
$h( n) =2n.$
Proof. The proof is by induction on
![]() $n.$
For
$n.$
For
![]() $n=1,5$
and
$n=1,5$
and
![]() $6,\ h( n) =2n;$
and for
$6,\ h( n) =2n;$
and for
![]() $ n=2,3$
and
$ n=2,3$
and
![]() $4,\ h( n) =2n-1.$
So conditions (a) to (d) hold for these minimal values of
$4,\ h( n) =2n-1.$
So conditions (a) to (d) hold for these minimal values of
![]() $n.$
Assume conditions (a) to (d) for values less than some
$n.$
Assume conditions (a) to (d) for values less than some
![]() $n.$
Suppose
$n.$
Suppose
![]() $ n=2^{k}( 4q+1)>3$
and let
$ n=2^{k}( 4q+1)>3$
and let
![]() $q=\sum _{i=1}^{r}2^{q_{i}}.$
Then
$q=\sum _{i=1}^{r}2^{q_{i}}.$
Then
 $$ \begin{align*} n=2^{k}+\sum_{i=1}^{r}2^{q_{i}+k+2} \end{align*} $$
$$ \begin{align*} n=2^{k}+\sum_{i=1}^{r}2^{q_{i}+k+2} \end{align*} $$
and
 $$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +\sum_{j=1}^{n-2^{q_{1}+k+2}}g( 2^{q_{1}+k+2}+j). \end{align*} $$
$$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +\sum_{j=1}^{n-2^{q_{1}+k+2}}g( 2^{q_{1}+k+2}+j). \end{align*} $$
If
![]() $q_{2}<q_{1}-1$
, then
$q_{2}<q_{1}-1$
, then
![]() $n-2^{q_{1}+k+2}<2^{q_{1}+k+1},$
so by Theorem 2.2(b) and (d),
$n-2^{q_{1}+k+2}<2^{q_{1}+k+1},$
so by Theorem 2.2(b) and (d),
and
 $$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +1+\sum_{j=1}^{n-2^{q_{1}+k+2}}g( j) =h( 2^{q_{1}+k+2}) +1+h( n-2^{q_{1}+k+2}). \end{align*} $$
$$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +1+\sum_{j=1}^{n-2^{q_{1}+k+2}}g( j) =h( 2^{q_{1}+k+2}) +1+h( n-2^{q_{1}+k+2}). \end{align*} $$
So by the induction hypothesis, if
![]() $k>0,$
$k>0,$
If
![]() $q_{2}=q_{1}-1,$
by Theorem 2.2(e), (b) and (f),
$q_{2}=q_{1}-1,$
by Theorem 2.2(e), (b) and (f),
 $$ \begin{align*} g( 2^{q_{1}+k+2}+2^{q_{2}+k+2}) & =3=g( 2^{q_{2}+k+2})+1 \\ g( 2^{q_{1}+k+2}+2^{q_{2}+k+2}+1) & =2=g(2^{q_{2}+k+2}+1) -1. \end{align*} $$
$$ \begin{align*} g( 2^{q_{1}+k+2}+2^{q_{2}+k+2}) & =3=g( 2^{q_{2}+k+2})+1 \\ g( 2^{q_{1}+k+2}+2^{q_{2}+k+2}+1) & =2=g(2^{q_{2}+k+2}+1) -1. \end{align*} $$
So by Theorem 2.2
![]() $(d)$
, for the other values of
$(d)$
, for the other values of
![]() $j,$
$j,$
 $$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +1+\sum_{j=1}^{n-2^{q_{1}+k+2}}g( j) =2n-1 \end{align*} $$
$$ \begin{align*} h( n) =\sum_{j=1}^{2^{q_{1}+k+2}}g( j) +1+\sum_{j=1}^{n-2^{q_{1}+k+2}}g( j) =2n-1 \end{align*} $$
as before, so we have condition (b). If, instead,
![]() $k=0,$
the induction hypothesis gives
$k=0,$
the induction hypothesis gives
then we have condition (a). If
![]() $n=2^{k}( 4q+3)$
, the working is as above, except that the induction hypothesis gives, for
$n=2^{k}( 4q+3)$
, the working is as above, except that the induction hypothesis gives, for
![]() $k>0,$
$k>0,$
and for
![]() $k=0,$
$k=0,$
so we have conditions (d) and (c).
Theorem 3.3 (Limits on
 $h(n)$
).
$h(n)$
).
If
![]() $h( n) +1\neq 2, 7\pmod 8$
, then
$h( n) +1\neq 2, 7\pmod 8$
, then
![]() $g( h( n) +1) =2$
and for no other values of m is
$g( h( n) +1) =2$
and for no other values of m is
![]() $g( m) =2.$
$g( m) =2.$
Proof. If
![]() $n=4q+1,$
by Theorem 3.2(a),
$n=4q+1,$
by Theorem 3.2(a),
![]() $h( n) +1=2n+1=8q+3$
. So by Theorem 2.1(iv), we have the result.
$h( n) +1=2n+1=8q+3$
. So by Theorem 2.1(iv), we have the result.
If
![]() $n=2^{k}( 4q+1) $
and
$n=2^{k}( 4q+1) $
and
![]() $k>0,$
by Theorem 3.2(b),
$k>0,$
by Theorem 3.2(b),
![]() $h( n) +1=2n=2^{k+1}( 4q+1)$
and we have the result by Theorem 2.1(viii) if
$h( n) +1=2n=2^{k+1}( 4q+1)$
and we have the result by Theorem 2.1(viii) if
![]() $k>1,$
and by Theorem 2.1(v) if
$k>1,$
and by Theorem 2.1(v) if
![]() $k=1.$
$k=1.$
If
![]() $n=4q+3,$
by Theorem 3.2(c),
$n=4q+3,$
by Theorem 3.2(c),
![]() $h( n) +1=2n=8q+6$
. So by Theorem 2.1(vii), we have the result.
$h( n) +1=2n=8q+6$
. So by Theorem 2.1(vii), we have the result.
If
![]() $n=2^{k}( 4q+3) ,$
by Theorem 3.2(d),
$n=2^{k}( 4q+3) ,$
by Theorem 3.2(d),
![]() $h( n) +1=2n+1=2^{k+3}q+2^{k+2}+2^{k+1}+1$
. So by Theorem 2.2(j),
$h( n) +1=2n+1=2^{k+3}q+2^{k+2}+2^{k+1}+1$
. So by Theorem 2.2(j),
![]() $g( h( n) +1) =g( 2^{k+2}+2^{k+1}+1)$
and the result follows from Theorem 2.2(f).
$g( h( n) +1) =g( 2^{k+2}+2^{k+1}+1)$
and the result follows from Theorem 2.2(f).
By Theorem 3.2, the value of
![]() $g( m) $
when
$g( m) $
when
![]() ${m=8q+7}$
or
${m=8q+7}$
or
![]() $ 8q+2 $
is
$ 8q+2 $
is
![]() $1$
, and for
$1$
, and for
![]() ${m=8q+1,}\ 2^{k+1}( 4q+3) $
with
${m=8q+1,}\ 2^{k+1}( 4q+3) $
with
![]() $k>0$
or
$k>0$
or
![]() $ 2^{k+1}( 4q+1) +1$
with
$ 2^{k+1}( 4q+1) +1$
with
![]() $k>0,\ g( m) =3.$
$k>0,\ g( m) =3.$
Summarising,
![]() $g( m) =2,$
where
$g( m) =2,$
where
![]() $m=8q+3,\ 8q+6,\ 2^{k+1}( 4q+1) $
with
$m=8q+3,\ 8q+6,\ 2^{k+1}( 4q+1) $
with
![]() $k>0$
and
$k>0$
and
![]() $2^{k+1}( 4q+3) +1$
with
$2^{k+1}( 4q+3) +1$
with
![]() $k>0.$
So all the cases when
$k>0.$
So all the cases when
![]() $g( m) =2$
are obtained when
$g( m) =2$
are obtained when
![]() ${m=h( n) +1}.$
${m=h( n) +1}.$
4. Confirmation of Hendriks’s conjecture
We are now able to state our main result, namely that the sequence
![]() $ {A=a( 1) a( 2) a( 3) \ldots } $
of A088431 is exactly the sequence
$ {A=a( 1) a( 2) a( 3) \ldots } $
of A088431 is exactly the sequence
![]() $G=g( 1) g( 2) g( 3)\ldots .$
$G=g( 1) g( 2) g( 3)\ldots .$
Theorem 4.1 (Confirmation of Hendriks’s conjecture).
The sequences A and G are the same, that is,
![]() $a( n) =g(n) $
.
$a( n) =g(n) $
.
Proof. By Theorem 2.2(c),
![]() $g( 2^{n}-i) =g( i)$
for
$g( 2^{n}-i) =g( i)$
for
![]() $0\leq i<2^{n-1}-1,$
and
$0\leq i<2^{n-1}-1,$
and
Let
![]() $G_{n}^{R+1}$
denote the reverse of
$G_{n}^{R+1}$
denote the reverse of
![]() $G_{n}$
with a
$G_{n}$
with a
![]() $1$
added to the new first term. Then
$1$
added to the new first term. Then
Since
![]() $G_{5}$
has the subsequences:
$G_{5}$
has the subsequences:
![]() $321,123,1223,3221,212,312,232$
and
$321,123,1223,3221,212,312,232$
and
![]() $231.$
Thus,
$231.$
Thus,
![]() $321$
and
$321$
and
![]() $213$
will appear in
$213$
will appear in
![]() $G_{5}^{R+1}$
and so in
$G_{5}^{R+1}$
and so in
![]() $G_{6}.$
For
$G_{6}.$
For
![]() $ n>3,$
$ n>3,$
so the middle sequence of any
![]() $G_{n}$
will be
$G_{n}$
will be
![]() $232.$
No new sequence of this kind can be generated in any
$232.$
No new sequence of this kind can be generated in any
![]() $G_{n}$
or
$G_{n}$
or
![]() $G_{n}^{R+1}.$
Leaving out all the
$G_{n}^{R+1}.$
Leaving out all the
![]() $ 2\mathrm{s}$
in
$ 2\mathrm{s}$
in
![]() $G,$
every
$G,$
every
![]() $1$
is followed by a
$1$
is followed by a
![]() $3$
and every
$3$
and every
![]() $3$
is followed by a
$3$
is followed by a
![]() $ 1,$
giving
$ 1,$
giving
![]() $1,3,1,3,\ldots .$
By Theorem 3.3,
$1,3,1,3,\ldots .$
By Theorem 3.3,
![]() $\ g( n) $
has the defining properties of
$\ g( n) $
has the defining properties of
![]() $a(n)$
given at Definition 1.2.
$a(n)$
given at Definition 1.2.
The referee advised us of the existence of the free software Walnut, which is described by Shallit [Reference Shallit12]. Walnut can decide first-order predicates about automatic sequences, including the paperfolding sequence. The referee confirmed Theorem 4.1 using Walnut code. Walnut is authored by Hamoon Mousavi, and has been used extensively in confirming features of sequences found in the Online Encyclopedia of Integer Sequences (OEIS).
5. Summed paperfolding and continued fractions
There is an interesting connection between continued fractions and summed paperfolding. Shallit [Reference Shallit11] identifies the continued fraction expansion of
![]() $\sum _{k=0}^{u+1}{1}/{m^{2^{k}}}$
for m an integer greater than
$\sum _{k=0}^{u+1}{1}/{m^{2^{k}}}$
for m an integer greater than
![]() $1$
, once the continued fraction expansion of
$1$
, once the continued fraction expansion of
![]() $\sum _{k=0}^{u} {1}/{m^{2^{k}}}$
is known. Thus, if
$\sum _{k=0}^{u} {1}/{m^{2^{k}}}$
is known. Thus, if
 $$ \begin{align*} \sum_{k=0}^{u}\frac{1}{m^{2^{k}}}=[a_{0};a_{1},\ldots ,a_{n}], \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{u}\frac{1}{m^{2^{k}}}=[a_{0};a_{1},\ldots ,a_{n}], \end{align*} $$
then
 $$ \begin{align*} \sum_{k=0}^{u+1}\frac{1}{m^{2^{k}}}=[a_{0};a_{1},\ldots ,a_{n-1},a_{n}+1,a_{n}-1,a_{n}-1,a_{n-1},a_{n-2},\ldots ,a_{2},a_{1}]. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{u+1}\frac{1}{m^{2^{k}}}=[a_{0};a_{1},\ldots ,a_{n-1},a_{n}+1,a_{n}-1,a_{n}-1,a_{n-1},a_{n-2},\ldots ,a_{2},a_{1}]. \end{align*} $$
He acknowledges that for
![]() $m=2,$
which is the focus of our attention, the expansion contains a number of terms having value
$m=2,$
which is the focus of our attention, the expansion contains a number of terms having value
![]() $0.$
This is not problematic as the following equality allows for the conversion of such continued fractions:
$0.$
This is not problematic as the following equality allows for the conversion of such continued fractions:
He also shows that
![]() $\sum _{k=0}^{\infty }1/m^{2^k}$
for
$\sum _{k=0}^{\infty }1/m^{2^k}$
for
![]() $m\geq 2$
is irrational and proves some interesting results relating to the partial denominators of its continued fraction.
$m\geq 2$
is irrational and proves some interesting results relating to the partial denominators of its continued fraction.
Pethö [Reference Pethö10] generalises the method found by Shallit [Reference Shallit11] to develop a continued fraction expansion for Fredholm numbers of the second kind. The number
![]() $\sum _{k=0}^{\infty }{1}/{2^{2^{k}}},$
upon which the summed paperfolding sequence is based, is an example of a Fredholm number of the second kind.
$\sum _{k=0}^{\infty }{1}/{2^{2^{k}}},$
upon which the summed paperfolding sequence is based, is an example of a Fredholm number of the second kind.
Acknowledgement
We thank the referee for insightful comments and helpful suggestions which have enhanced the presentation of our results. We were delighted to learn that the open source software programme Walnut confirmed our results.